题目内容
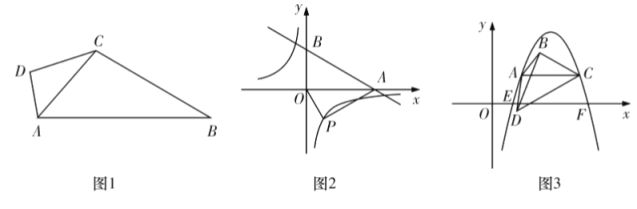
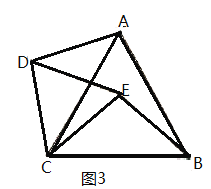
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=ABAD.
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求AF的值.
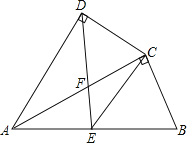
【答案】(1)详见解析;(2)详见解析;(3)AF=![]() .
.
【解析】
(1)先根据角平分线得出∠CAD=∠CAB,进而判断出△ADC∽△ACB,即可得出结论;
(2)先利用直角三角形的性质得出CE=AE,进而得出∠ACE=∠CAE,从而∠CAD=∠ACE,即可得出结论;
(3)由(1)的结论求出AC,再求出CE=3,最后由(2)的结论得出△CFE∽△AFD,即可得出结论.
解:(1)∵AC平分∠BAD,
∴∠CAD=∠CAB,
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴![]() ,
,
∴AC2=ADAB;
(2)在Rt△ABC中,∵E为AB的中点,
∴CE=AE(直角三角形斜边的中线等于斜边的一半),
∴∠ACE=∠CAE,
∵AC平分∠BAD,
∴∠CAD=∠CAE,
∴∠CAD=∠ACE,
∴CE∥AE;
(3)由(1)知,AC2=ADAB,
∵AD=4,AB=6,
∴AC2=4×6=24,
∴AC=2![]() ,
,
在Rt△ABC中,∵E为AB的中点,
∴CE=![]() AB=3,
AB=3,
由(2)知,CE∥AD,
∴△CFE∽△AFD,
∴![]() ,
,
∴![]() ,
,
∴AF=![]() .
.

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目