Question

【题目】如图，△ABC内接于⊙O，点D在AB边上，CD与OB交于点E，∠ACD＝∠OBC；

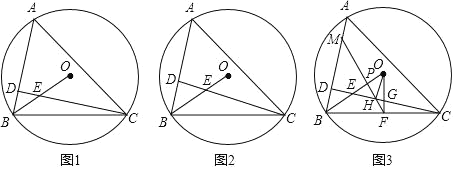
（1）如图1，求证：CD⊥AB；

（2）如图2，当∠BAC＝∠OBC+∠BCD时，求证：BO平分∠ABC；

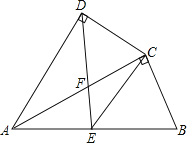
（3）如图3，在（2）的条件下，作OF⊥BC于点F，交CD于点G，作OH⊥CD于点H，连接FH并延长，交OB于点P，交AB边于点M．若OF＝3，MH＝5，求AC边的长．

Answer 1

【答案】（1）见解析；（2）见解析；（3）AC＝

【解析】

（1）根据直径所对的圆周角是直角，得出∠FCB=90°，再根据“同弧所对的圆周角相等”得出∠A=∠F，再根据已知条件得∠3=90°，得CD⊥AB；
（2）延长BO交AC于K，由已知可得∠A=∠5，由∠A+∠2=90°得∠5+∠2=90°，根据三角形的内角和定理及外角定理得出∠9=∠1得出BO平分∠ABC；
（3）延长BO交AC于点K，延长CD交⊙O于点N，联结BN，由条件可得CH=NH，BF=CF，从而HF是△CBN的中位线，HF∥BN，得出∠OEH=∠EHM又由∠OEH+∠EOH=∠EHM+∠OHP=90°可得HM=OB=5，在Rt△OBF中，根据勾股定理可得BF=4，解出BC=8，sin∠OBC=，所以可得AC=2CK，CK=BCsin∠OBC=得AC=.

解：（1）如图1，令∠OBC＝∠1，∠ACD＝∠2

延长BO交⊙O于F，连接CF．

∵BF是⊙O的直径，∴∠FCB＝90°

∴∠1+∠F＝90°，

∵弧BC＝弧BC，

∴∠A＝∠F

又∵∠1＝∠2，

∴∠2+∠A＝90°，

∴∠3＝90°，

∴CD⊥AB

（2）如图2，令∠OBC＝∠1，∠BCD＝∠4

延长BO交AC于K

∵∠A＝∠1+∠4，∠5＝∠1+∠4，

∴∠A＝∠5，

∵∠A+∠2＝90°，

∴∠5+∠2＝90°，

∴∠6＝90°

∵∠7＝180°﹣∠3＝90°，

∴∠6＝∠7，

又∵∠5＝∠8，∴∠9＝∠2

∵∠2＝∠1，∴∠9＝∠1，

∴BO平分∠ABC

（3）如图3，延长BO交AC于点K，延长CD交⊙O于点N，联结BN

∵OH⊥CN，OF⊥BC

∴CH＝NH，BF＝CF

∴HF是△CBN的中位线，HF∥BN

∴∠FHC＝∠BNC＝∠BAC

∵∠BAC＝∠OEH，∠FHC＝∠EHM

∴∠OEH＝∠EHM

设EM、OE交于点P

∵∠OEH+∠EOH＝∠EHM+∠OHP＝90°

∴∠EOH＝∠OHP

∴OP＝PH

∵∠ADC＝∠OHC＝90°

∴AD∥OH

∴∠PBM＝∠EOH，∠BMP＝∠OHP

∴PM＝PB

∴PM+PH＝PB+OP

∴HM＝OB＝5

在Rt△OBF中，根据勾股定理可得BF＝4

∴BC＝8，sin∠OBC＝

∵∠A+∠ABO＝∠DEB+∠ABO＝90°

∴∠AKB+∠CKB＝90°

∴OK⊥AC

AC＝2CK，CK＝BCsin∠OBC＝

∴AC＝