Question

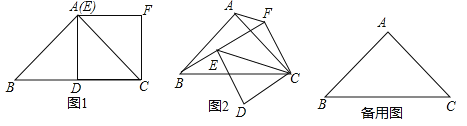
【题目】从三角形(不是等腰三角形)一个顶点引出一条射线 与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线．

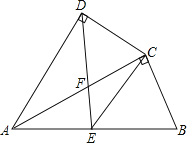
如图1，在中，是的完美分割线，且， 则的度数是

如图2，在中，为角平分线，，求证: 为的完美分割线．

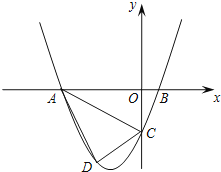
如图2，中，是的完美分割线，且是以为底边的等腰三角形，求完美分割线的长．

Answer 1

【答案】（1）88°；（2）详见解析；（3）

【解析】

（1）是的完美分割线，且，得∠ACD=44°，∠BCD=44°，进而即可求解；

（2）由，得，由平分，，得为等腰三角形，结合，即可得到结论；

（3）由是的完美分割线，得从而得，设，列出方程，求出x的值，再根据，即可得到答．

(1) ∵是的完美分割线，且，

∴，∠A=∠ACD=44°，

∴∠A=∠BCD=44°，

∴．

故答案是：88°；

，

，

不是等腰三角形，

平分，

，

，

为等腰三角形．

，，

，

是的完美分割线．

∵是以为底边的等腰三角形，

∴，

∵是的完美分割线，

∴

，

设，则，

，

，

．