题目内容
(2013•崇明县一模)已知:如果抛物线y=ax2+bx+c的顶点为B(3,-4),且经过点C(0,5).
(1)求抛物线的函数关系式;
(2)若过点C的直线y=kx+b与抛物线相交于点E(4,m),求△CBE的面积.
(1)求抛物线的函数关系式;
(2)若过点C的直线y=kx+b与抛物线相交于点E(4,m),求△CBE的面积.
分析:(1)利用顶点式直接将B(3,-4),代入得出y=a(x-3)2-4,进而求出抛物线的函数关系式;
(2)根据抛物线y=(x-3)2-4过点E(4,m),即可得出m的值,进而得出S△BEF,S△CBF,求出△CBE的面积即可.
(2)根据抛物线y=(x-3)2-4过点E(4,m),即可得出m的值,进而得出S△BEF,S△CBF,求出△CBE的面积即可.
解答: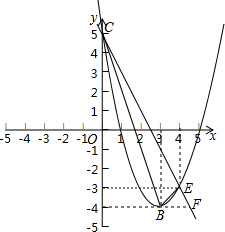 解:(1)设抛物线的解析式为y=a(x-3)2-4,
解:(1)设抛物线的解析式为y=a(x-3)2-4,
将C(0,5)代入y=a(x-3)2-4得,
a=1,
抛物线的函数关系式:y=(x-3)2-4;
(2)∵抛物线y=(x-3)2-4过点E(4,m),
∴m=1-4=-3,
∴E(4,-3),
∵E(4,-3),C(0,5),
∴
,
解得:
,
∴直线解析式为:y=-2x+5,
过点B作y轴的垂线,并反向延长交直线y=kx+b与点F,
此时B点坐标为(3,-4),
则y=-4,-4=-2x+5,
解得:x=4.5,
故BF=4.5-3=1.5,
S△BEF=
×1.5×1=
,
S△CBF=
×9×1.5=
,
∴△CBE的面积为:
-
=6.
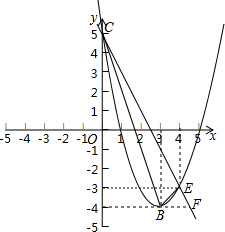 解:(1)设抛物线的解析式为y=a(x-3)2-4,
解:(1)设抛物线的解析式为y=a(x-3)2-4,将C(0,5)代入y=a(x-3)2-4得,
a=1,
抛物线的函数关系式:y=(x-3)2-4;
(2)∵抛物线y=(x-3)2-4过点E(4,m),
∴m=1-4=-3,
∴E(4,-3),
∵E(4,-3),C(0,5),
∴
|
解得:
|
∴直线解析式为:y=-2x+5,
过点B作y轴的垂线,并反向延长交直线y=kx+b与点F,
此时B点坐标为(3,-4),
则y=-4,-4=-2x+5,
解得:x=4.5,
故BF=4.5-3=1.5,
S△BEF=
| 1 |
| 2 |
| 3 |
| 4 |
S△CBF=
| 1 |
| 2 |
| 27 |
| 4 |
∴△CBE的面积为:
| 27 |
| 4 |
| 3 |
| 4 |
点评:此题主要考查了利用顶点式求二次函数解析式以及两图象交点求法等知识,根据已知得出BF的长是解题关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目
 (2013•崇明县一模)已知二次函数y=ax2+bx+c的图象如图所示,那么a,b,c的符号为( )
(2013•崇明县一模)已知二次函数y=ax2+bx+c的图象如图所示,那么a,b,c的符号为( ) (2013•崇明县一模)如图,在航线l的两侧分别有观测点A和B,点A到航线l的距离为2海里,点B位于点A北偏东60°方向且与A相距l0海里处.现有一艘轮船从位于点B南偏西76°方向的C处,正沿该航线自西向东航行,10分钟后该轮船行至点A的正北方向的D处.
(2013•崇明县一模)如图,在航线l的两侧分别有观测点A和B,点A到航线l的距离为2海里,点B位于点A北偏东60°方向且与A相距l0海里处.现有一艘轮船从位于点B南偏西76°方向的C处,正沿该航线自西向东航行,10分钟后该轮船行至点A的正北方向的D处.