Question

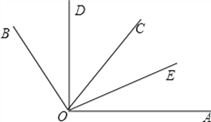
【题目】如图，OD平分∠BOC，OE平分∠AOC．若∠BOC=70°，∠AOC=50°．

（1）求出∠AOB及其补角的度数；

（2）请求出∠DOC和∠AOE的度数，并判断∠DOE与∠AOB是否互补，并说明理由.

Answer 1

【答案】（1）120°，60°；（2）∠DOE与∠AOB互补，理由见解析.

【解析】试题分析：（1）∠AOB的度数等于已知两角的和，再根据补角的定义求解；

（2）根据角平分线把角分成两个相等的角，求出度数后即可判断．

试题解析：解：（1）∠AOB=∠BOC+∠AOC=70°+50°=120°，

其补角为180°-∠AOB=180°-120°=60°.

（2）∠DOC=∠BOC=×70°=35°，∠AOE=∠AOC=×50°=25°.

∠DOE与∠AOB互补.理由如下：

∵∠DOC=35°，∠AOE=25°，

∴∠DOE=∠DOC+∠COE =∠DOC+∠AOE=60°.

∴∠DOE+∠AOB=60°+120°=180°，

∴∠DOE与∠AOB互补.