题目内容
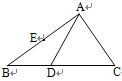
【题目】如图,△ABC中,D为BC边上的点,∠CAD=∠CDA,E为AB边的中点.
(1)尺规作图:作∠C的平分线CF,交AD于点F(保留作图痕迹,不写作法);
(2)连结EF,EF与BC是什么位置关系?为什么?
(3)若四边形BDFE的面积为9,求△ABD的面积.
【答案】(1)作图见解析;
(2)EF∥BC,原因见解析;
(3)△ABD的面积为12
【解析】(本小题满分12分)
解:(1)尺规作图略;…………………………………………………………3分
(2)EF∥BC(即EF平行于BC).……………………………………1分
原因如下:如图1,∵∠CAD=∠CDA,
∴AC=DC(等角对等边),即△CAD为等腰三角形;…………………2分
又CF是顶角∠ACD的平分线,由“三线合一”定理,
知CF是底边AD的中线,即F为AD的中点,……………………………3分
结合E是AB的中点,得EF为△ABD的中位线,………………………4分
∴EF∥BD,从而EF∥BC;……………………………………………5分
(3)由(2)知EF∥BC,∴△AEF∽△ABD,…………………1分
∴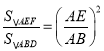 ,……………………………………………………………2分
,……………………………………………………………2分
又∵AE=![]() AB,∴得
AB,∴得![]() ,
,
把S四边形BDFE=9代入其中,解得
S△AEF=3,………………………………………………………………………3分
∴S△ABD=S△AEF+S四边形BDFE=3+9=12,……………………………4分
即△ABD的面积为12.

练习册系列答案
相关题目