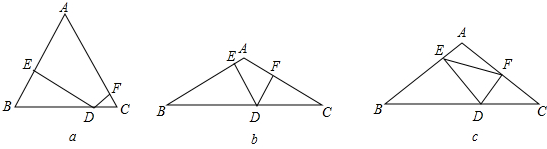
题目内容
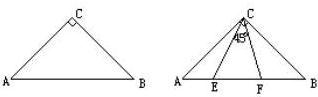
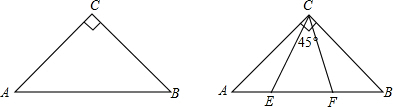
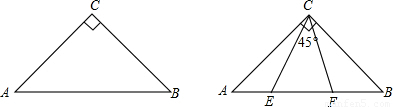
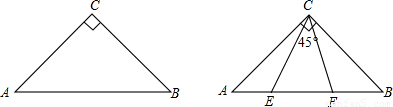
已知△ABC是等腰三角形,AB=AC,D为边BC上任意一点,DE⊥AB于E,DF⊥AC于F,且E,F分别在边AB,AC上.
(1)如图a,当△ABC是等边三角形时,证明:AE+AF= BC.
BC.
(2)如图b,若△ABC中,∠BAC=120°,探究线段AE,AF,AB之间的数量关系,并对你的猜想加以证明.
(3)如图c,若△ABC中,AB=10,BC=16,EF=6,利用你对(1),(2)两题的解题思路计算出线段CD(BD>CD)的长.
(1)证明:∵△ABC是等边三角形,DE⊥AB于E,DF⊥AC于F,
∴∠EDB=∠FDC=30°,
∴EB= BD,FC=
BD,FC= CD,
CD,
∴BE+FC= BD+
BD+ CD=
CD= BC,
BC,
∴AE+AF=AB+AC-BE-FC=2BC- BC,
BC,
∴AE+AF= BC;
BC;
(2)解:AE+AF= AB.
AB.
理由:∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∴BE=BD•cos30°,CF=CD•cos30°,
∴AE+AF=AB-BE+AC-CF,
=2AB-BD•cos30°-CD•cos30°,
=2AB-BC•cos30°,
=2AB-2AB•cos30°×cos30°,
= AB,
AB,
即AE+AF= AB;
AB;
(3)解:过点A作AM⊥BC于点M,
∵AC=AB=10,BC=16,EF=6,
∴BM=CM=8,
由勾股定理得,AM= =
=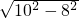 =6,
=6,
∵DE⊥AB,DF⊥AC,
∴在Rt△BDE中,BE=BD•cos∠B=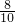 BD=
BD= BD,
BD,
在Rt△CDF中,CF=CD•cos∠C=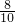 CD=
CD= CD,
CD,
∴BE+CF= (BD+CD)=
(BD+CD)= BC=
BC= ×16=
×16=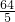 ,
,
∴AE+AF=AB+AC-(BE+CF)=2×10-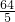 =
=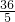 ,
,
过点F作FG⊥BA的延长线于G,过点C作CN⊥BA的延长线于N,
则S△ABC= AB•CN=
AB•CN= BC•AM,
BC•AM,
即 ×10•CN=
×10•CN= ×16×6,
×16×6,
解得CN=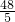 ,
,
由勾股定理,AN= =
= =
= ,
,
∴sin∠CAN=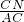 =
= =
=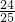 ,
,
cos∠CAN=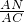 =
= =
=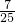 ,
,
设AF=x,则AE=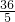 -x,
-x,
在Rt△AFG中,FG=AF•sin∠CAN=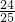 x,
x,
AG=AF•cos∠CAN=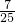 x,
x,
∴EG=AE+AG=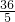 -x+
-x+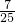 x=
x=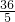 -
-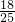 x,
x,
在Rt△EFG中,EF2=EG2+FG2,
即62=(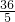 -
-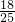 x)2+(
x)2+(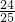 x)2,
x)2,
整理得,5x2-36x+55=0,
解得x1=5,x2=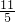 ,
,
∵BD>CD,
∴AF=AE=5,
∴CF=AC-AF=10-5=5,
CD=CF÷cos∠C=5÷ =
=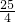 .
.
分析:(1)根据等边三角形的性质求出∠EDB=∠FDC=30°,再根据直角三角形30°角所对的直角边等于斜边的一半可得EB= BD,FC=
BD,FC= CD,然后表示出AE+AF即可;
CD,然后表示出AE+AF即可;
(2)根据等腰三角形两底角相等求出∠B=∠C=30°,然后解直角三角形表示出BE、CF,再表示出AE+AF整理即可得解;
(3)过点A作AM⊥BC于M,根据等腰三角形的性质求出BM,再利用勾股定理列式求出AM,根据(2)的思路求出AE+AF,过点F作FG⊥BA的延长线于G,过点C作CN⊥BA的延长线于N,利用△ABC的面积求出CN,再利用勾股定理列式求出AN,设AF=x,然后解直角三角形表示出AG、FG,然后表示出EG,在Rt△EFG中,利用勾股定理列出方程求出x,再求出CF,然后解直角三角形即可得到CD.
点评:本题考查了等边三角形的性质,等腰三角形等边对等角的性质,勾股定理的应用以及解直角三角形,读懂题目信息理清求解AE+AF的思路是解题的关键,(3)题较为复杂,作辅助线构造出直角三角形并利用勾股定理列出方程,然后求出AF的长是解题的关键.
∴∠EDB=∠FDC=30°,
∴EB=
 BD,FC=
BD,FC= CD,
CD,∴BE+FC=
 BD+
BD+ CD=
CD= BC,
BC,∴AE+AF=AB+AC-BE-FC=2BC-
 BC,
BC,∴AE+AF=
 BC;
BC;(2)解:AE+AF=
 AB.
AB.理由:∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∴BE=BD•cos30°,CF=CD•cos30°,
∴AE+AF=AB-BE+AC-CF,
=2AB-BD•cos30°-CD•cos30°,
=2AB-BC•cos30°,
=2AB-2AB•cos30°×cos30°,
=
 AB,
AB,即AE+AF=
 AB;
AB;(3)解:过点A作AM⊥BC于点M,
∵AC=AB=10,BC=16,EF=6,
∴BM=CM=8,
由勾股定理得,AM=
 =
=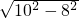 =6,
=6,∵DE⊥AB,DF⊥AC,
∴在Rt△BDE中,BE=BD•cos∠B=
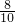 BD=
BD= BD,
BD,在Rt△CDF中,CF=CD•cos∠C=
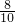 CD=
CD= CD,
CD,
∴BE+CF=
 (BD+CD)=
(BD+CD)= BC=
BC= ×16=
×16=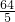 ,
,∴AE+AF=AB+AC-(BE+CF)=2×10-
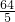 =
=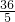 ,
,过点F作FG⊥BA的延长线于G,过点C作CN⊥BA的延长线于N,
则S△ABC=
 AB•CN=
AB•CN= BC•AM,
BC•AM,即
 ×10•CN=
×10•CN= ×16×6,
×16×6,解得CN=
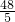 ,
,由勾股定理,AN=
 =
= =
= ,
,∴sin∠CAN=
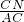 =
= =
=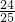 ,
,cos∠CAN=
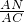 =
= =
=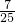 ,
,设AF=x,则AE=
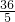 -x,
-x,在Rt△AFG中,FG=AF•sin∠CAN=
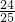 x,
x,AG=AF•cos∠CAN=
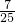 x,
x,∴EG=AE+AG=
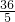 -x+
-x+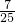 x=
x=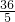 -
-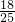 x,
x,在Rt△EFG中,EF2=EG2+FG2,
即62=(
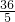 -
-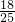 x)2+(
x)2+(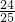 x)2,
x)2,整理得,5x2-36x+55=0,
解得x1=5,x2=
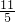 ,
,∵BD>CD,
∴AF=AE=5,
∴CF=AC-AF=10-5=5,
CD=CF÷cos∠C=5÷
 =
=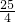 .
.分析:(1)根据等边三角形的性质求出∠EDB=∠FDC=30°,再根据直角三角形30°角所对的直角边等于斜边的一半可得EB=
 BD,FC=
BD,FC= CD,然后表示出AE+AF即可;
CD,然后表示出AE+AF即可;(2)根据等腰三角形两底角相等求出∠B=∠C=30°,然后解直角三角形表示出BE、CF,再表示出AE+AF整理即可得解;
(3)过点A作AM⊥BC于M,根据等腰三角形的性质求出BM,再利用勾股定理列式求出AM,根据(2)的思路求出AE+AF,过点F作FG⊥BA的延长线于G,过点C作CN⊥BA的延长线于N,利用△ABC的面积求出CN,再利用勾股定理列式求出AN,设AF=x,然后解直角三角形表示出AG、FG,然后表示出EG,在Rt△EFG中,利用勾股定理列出方程求出x,再求出CF,然后解直角三角形即可得到CD.
点评:本题考查了等边三角形的性质,等腰三角形等边对等角的性质,勾股定理的应用以及解直角三角形,读懂题目信息理清求解AE+AF的思路是解题的关键,(3)题较为复杂,作辅助线构造出直角三角形并利用勾股定理列出方程,然后求出AF的长是解题的关键.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目