Question

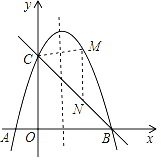
【题目】如图，二次函数y=ax2+bx+c（a≠0）的图象的顶点C的坐标为（﹣1，﹣3），与x轴交于A（﹣3，0）、B（1，0），根据图象回答下列问题：

（1）写出方程ax2+bx+c=0的根；

（2）写出不等式ax2+bx+c＞0的解集；

（3）若方程ax2+bx+c=k有实数根，写出实数k的取值范围．

Answer 1

【答案】（1）x1=-3、x2=1；（2）x＜-3或x＞1；（3）k≥-3．

【解析】试题分析：

（1）一元二次方程ax2+bx+c=0的根是二次函数y=ax2+bx+c（a≠0）的图象与x轴交点

的横坐标可得答案；

（2）由不等式ax2+bx+c＞0的解集是抛物线位于横轴之上的部分图象所对应的自变量的取值可得解集；

（3）由方程ax2+bx+c=k有实数根，则抛物线y=ax2+bx+c（a≠0）与直线y=k有交点，结合抛物线y=ax2+bx+c（a≠0）的顶点坐标为（﹣1，﹣3）可得答案；

试题解析：

（1）∵方程ax2+bx+c=0的根是二次函数y=ax2+bx+c（a≠0）的图象与x轴交点的横坐标，
∴方程ax2+bx+c=0的根为x1=-3、x2=1；
（2）不等式ax2+bx+c＞0的解集是抛物线在x轴上方部分图象对应的x的范围，
∴不等式ax2+bx+c＞0的解集为x＜-3或x＞1；
（3）∵方程ax2+bx+c=k有实数根，
∴抛物线y=ax2+bx+c与直线y=k有交点，
由函数图象知k≥-3．