题目内容
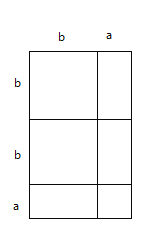
【题目】数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为a、宽为b的长方形.用A种纸片- -张,B种纸片一张,C种纸片两张可拼成如图2的大正方形.
(1)请用两种不同的方法求图2大正方形的面积(答案直接填写到题中横线上);
方法1_________________;
方法2______________________.
(2)观察图2,请你直接写出下列三个代数式: (a+b)2, a2+b2, ab之间的等量关系;
(3)类似的,请你用图1中的三种纸片拼一个图形验证: (a+b)(a+2b)=a2 + 3ab+2b2,请你将该示意图画在答题卡上;
(4)根据(2)题中的等量关系,解决如下问题:
①已知: a+b=5,a2+b2=11, 求ab的值:
②已知(x- 2018)2 +(x- 2020)2=34,求(x- 2019)2的值,

【答案】(1)a2+b2+2ab;(a+b)2;(2)(a+b)2=a2+2ab+b2;(3)见解析(4)①ab=7;②(x-2019)2=16
【解析】
(1)根据正方形的面积求法与割补法即可求解;
(2)根据完全平方公式即可求解;
(3)根据多项式的乘法即可画图;
(4)①根据完全平方公式的变形即可求解;②令x-2019=a,根据完全平方公式即可求解.
(1)图2大正方形的面积
方法一:a2+b2+2ab
方法二:(a+b)2;
(2)(a+b)2, a2+b2, ab之间的等量关系为(a+b)2=a2+2ab+b2;
(3)如图:(a+b)(a+2b)=a2 + 3ab+2b2,
(4)①∵a+b=5,a2+b2=11,
∴(a+b)2= a2+b2+2ab=25
即11+2ab=25,解得ab=7
②(x- 2018)2 +(x- 2020)2=34,
令x-2019=a,
故(a+1)2 +( a-1)2=34,
化简得2a2+2=34
∴a2=16
即(x-2019)2=16

 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案