题目内容
【题目】平面内的两条直线有相交和平行两种位置关系.
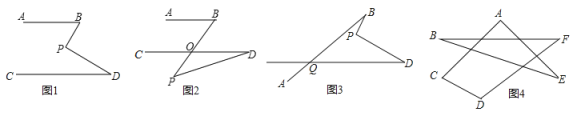
(1)如图1,若![]() ,点
,点![]() 在
在![]() 、
、![]() 内部,
内部,![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
(2)如图2,在AB∥CD的前提下,将点![]() 移到
移到![]() 、
、![]() 外部,则
外部,则![]() 、
、![]() 、
、![]() 之间有何数量关系?请证明你的结论.
之间有何数量关系?请证明你的结论.
(3)如图3,写出![]() 、
、![]() 、
、![]() 、
、![]() 之间的数量关系?(不需证明)
之间的数量关系?(不需证明)
(4)如图4,求出![]() 的度数.
的度数.
【答案】(1)80°;(2)∠B=∠D+∠BPD,证明见解析;(3)∠BPD=∠B+∠D+BQD;;(4)360°.
【解析】
(1)过P作平行于AB的直线,根据内错角相等可得出三个角的关系,然后将∠B=50°,∠D=30°代入,即可求∠BPD的度数;
(2)先由平行线的性质得到∠B=∠BOD,然后根据∠BOD是三角形OPD的一个外角,由此可得出三个角的关系;
(3)延长BP交QD于M,再根据三角形的一个外角等于与它不相邻的两个内角的和解答;
(4)根据三角形外角性质得出∠CMN=∠A+∠E,∠DNB=∠B+∠F,代入∠C+∠D+CMN+∠DNM=360°即可求出答案.
(1)如图1,过P点作PO∥AB,
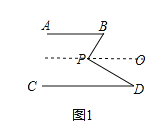
∵AB∥CD,∴CD∥PO∥AB,
∴∠BPO=∠B,∠OPD=∠D,
∵∠BPD=∠BPO+∠OPD,
∴∠BPD=∠B+∠D.
∵∠B=50°,∠D=30°,
∴∠BPD=∠B+∠D=50°+30°=80°;
(2)∠B=∠D+∠BPD,
∵AB∥CD,
∴∠B=∠BOD,
∵∠BOD=∠D+∠BPD,
∴∠B=∠D+∠BPD;
(3)如图:延长BP交QD于M
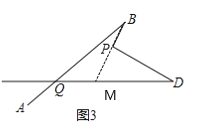
在△QBM中:∠BMD=∠BQD+∠QBM
在△PMD中:∠BPD=∠BMD+∠D=∠BQD+∠QBM+∠D
故答案为:∠BPD=∠B+∠D+BQD
∴![]() 、
、![]() 、
、![]() 、
、![]() 之间的数量关系为:∠BPD=∠B+∠D+BQD
之间的数量关系为:∠BPD=∠B+∠D+BQD
(4)如图
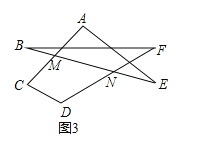
∵∠CMN=∠A+∠E,∠DNB=∠B+∠F,
又∵∠C+∠D+∠CMN+∠DNM=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.