题目内容
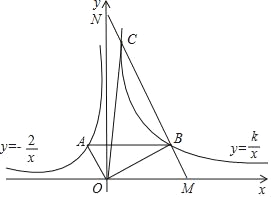
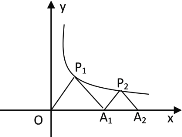
【题目】如图,ΔP1OA1,ΔP2A1A2是等腰直角三角形,点P1、P2在函数y=![]() (x>0)的图象上,斜边OA1、A1A2都在x轴上,则点A2的坐标是____________.
(x>0)的图象上,斜边OA1、A1A2都在x轴上,则点A2的坐标是____________.
【答案】(4![]() ,0)
,0)
【解析】
首先根据等腰直角三角形的性质,知点P1的横、纵坐标相等,再结合双曲线的解析式得到点P1的坐标是(2,2),则根据等腰三角形的三线合一求得点A1的坐标;同样根据等腰直角三角形的性质、点A1的坐标和双曲线的解析式求得A2点的坐标.
根据等腰直角三角形的性质,可设点P1(a,a),
又∵y=![]() ,∴a2=4,a=±2(负值舍去),
,∴a2=4,a=±2(负值舍去),
再根据等腰三角形的三线合一,得A1的坐标是(4,0),
设点P2的坐标是(4+b,b),又∵y=![]() ,则b(4+b)=4,
,则b(4+b)=4,
即b2+4b4=0,
又∵b>0,∴b=2![]() 2,
2,
再根据等腰三角形的三线合一,
∴4+2b=4+4![]() 4=4
4=4![]() ,
,
∴点A2的坐标是(4![]() ,0).
,0).

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
【题目】我市某中学举办“网络安全知识答题竞赛”,初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
平均分(分) | 中位数(分) | 众数(分) | 方差(分2) | |
初中部 | a | 85 | b | s初中2 |
高中部 | 85 | c | 100 | 160 |
(1)根据图示计算出a、b、c的值;
(2)结合两队成绩的平均数和中位数进行分析,哪个队的决赛成绩较好?
(3)计算初中代表队决赛成绩的方差s初中2,并判断哪一个代表队选手成绩较为稳定.