题目内容
【题目】如图,已知矩形ABCD的两条对角线相交于点O,过点A作AG⊥BD分别交BD、BC于点G、E. 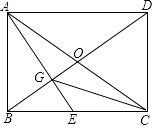
(1)求证:BE2=EGEA;
(2)连接CG,若BE=CE,求证:∠ECG=∠EAC.
【答案】
(1)证明:∵四边形ABCD是矩形,
∴∠ABC=90°,
∵AE⊥BD,
∴∠ABC=∠BGE=90°,
∵∠BEG=∠AEB,
∴△ABE∽△BGE,
∴ ![]() ,
,
∴BE2=EGEA
(2)证明:由(1)证得BE2=EGEA,
∵BE=CE,
∴CE2=EGEA,
∴ ![]() =
= ![]() ,
,
∵∠CEG=∠AEC,
∴△CEG∽△AEC,
∴∠ECG=∠EAC
【解析】(1)由四边形ABCD是矩形,得到∠ABC=90°,得到∠ABC=∠BGE=90°,根据相似三角形的性质即可得到结论;(2)由(1)证得BE2=EGEA,推出△CEG∽△AEC,根据相似三角形的性质即可得到结论.
【考点精析】本题主要考查了矩形的性质和相似三角形的判定与性质的相关知识点,需要掌握矩形的四个角都是直角,矩形的对角线相等;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.

【题目】某商场经营某种品牌的玩具,进价是20元,根据市场调查:在一段时间内,销售单价是30元时,销售量是500件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>30),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:
销售单价(元) | x |
销售量y(件) | |
销售玩具获得利润w(元) |
(2)在(1)问条件下,若商场获得了8000元销售利润,求该玩具销售单价x应定为多少元.
(3)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于35元,且商场要完成不少于350件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?