题目内容
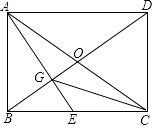
【题目】已知AB为⊙O的直径,C为⊙O上一点,AD与过C点的切线垂直,垂足为D,AD交⊙O于点E,∠CAB=30°
(1)如图①,求∠DAC的大小;
(2)如图②,若⊙O的半径为4,求DE的长.
【答案】
(1)解:连接OC,如图①,
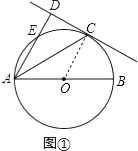
∵DC切⊙O于点C,∴OC⊥DC,又∵AD⊥DC,∴AD∥OC,∴∠DAC=∠ACO,∵OA=OC,∴∠OCA=∠CAB=30°,∴∠DAC=30°;
(2)解:连OE,OC,如图②,

∵∠EOC=2∠DAC=60°,∴△OEC为等边三角形,∴EC=OE=4,∠OCE=60°,∴∠DCE=30°,
∴DE= ![]() CE=2.
CE=2.
【解析】(1):连接OC根据切线的性质定理得出OC⊥DC,又AD⊥DC,根据同一平面内垂直于同一直线的两条直线互相平行得出AD∥OC,根据平行线的性质得出∠DAC=∠ACO,根据等边对等角得出∠OCA=∠CAB=30°,利用等量代换得出结论;
(2)连OE,OC,根据同弧所对的圆心角等于圆周角的2倍得出∠EOC=2∠DAC=60°,根据有一个角为60![]() 的等腰三角形是等边三角形得出△OEC为等边三角形,根据等边三角形三边相等得出EC=OE=4,然后利用含30
的等腰三角形是等边三角形得出△OEC为等边三角形,根据等边三角形三边相等得出EC=OE=4,然后利用含30![]() 角的直角三角形的边角关系得出DE的长。
角的直角三角形的边角关系得出DE的长。
【考点精析】关于本题考查的平行线的判定与性质和含30度角的直角三角形,需要了解由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质;在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半才能得出正确答案.

【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展,小明计划给朋友快递一部分物品,经了解有甲乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)根据题意,填写下表:
重量(千克) | 0.5 | 1 | 3 | 4 | … |
甲公司 | 22 | 67 | … | ||
乙公司 | 11 | 51 | … |
(2)请分别写出甲乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(3)小明应选择哪家快递公司更省钱?