Question

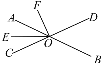
【题目】如图，已知直线AB和CD相交于点O，射线OE⊥AB于点O，射线OF⊥CD于点O，且∠AOF＝25°.求∠BOC与∠EOF的度数．

Answer 1

【答案】∠BOC＝115°, ∠EOF＝65°

【解析】

由OF⊥CD，得∠FOD=90°，已知∠AOF＝25°，从而由平角的性质可求得∠AOC的度数，然后由邻补角的性质可知∠BOC的度数，由OE⊥AB，∠AOE＝90°，可得∠FOE=∠AOE-∠AOF．

因为OF⊥CD，所以∠DOF＝90°.

因为∠AOC＋∠AOF＋∠DOF＝180°，

∠AOF＝25°，所以∠AOC＝65°.

因为∠AOC＋∠BOC＝180°，

所以∠BOC＝115°；

因为OE⊥AB，所以∠AOE＝90°，

所以∠AOF＋∠EOF＝90°.

因为∠AOF＝25°，所以∠EOF＝65°.

故答案为：∠BOC＝115°； ∠EOF＝65°.