题目内容
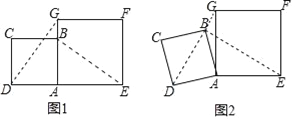
【题目】在数学兴趣小组活动中,小明进行数学探究活动,将边长为![]() 的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
(1)小明发现DG⊥BE,请你帮他说明理由;
(2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.
【答案】(1)见解析 (2)![]() +
+![]()
【解析】分析:(1)延长EB交DG于点H,先证出Rt△ADG≌Rt△ABE,得出∠AGD=∠AEB,再根据∠HBG=∠EBA,得出∠HGB+∠HBG=90°即可;
(2)过点A作AP⊥BD交BD于点P,根据△DAG≌△BAE得出DG=BE,根据AD=2∠PDA=45°,∠APD=90°,求出AP、DP,利用勾股定理求出PG,再根据DG=DP+PG求出DG,最后根据DG=BE即可得出答案.
详解:(1)如图1,延长EB交DG于点H,
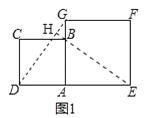
∵ABCD和AEFG为正方形,
∴在Rt△ADG和Rt△ABE中,
 ,
,
∴Rt△ADG≌Rt△ABE,
∴∠AGD=∠AEB,
∵∠HBG=∠EBA,
∴∠HGB+∠HBG=90°,
∴DG⊥BE;
(2)如图2,过点A作AP⊥BD交BD于点P,
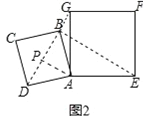
∵ABCD和AEFG为正方形,
∴在△DAG和△BAE中,
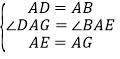 ,
,
∴△DAG≌△BAE(SAS),
∴DG=BE,
∵AD=2∠PDA=45°,∠APD=90°,
∴AP=DP=![]() ,
,
∵AG=2![]() ,∴PG=
,∴PG=![]() =
=![]() ,
,
∴DG=DP+PG=![]() +
+![]() ,
,
∵DG=BE,∴BE=![]() +
+![]() .
.

【题目】城区某中学为形成体育特色,落实学生每天![]() 小时的锻炼时间,通过调查研究,决定在七、八、九年级分别开展跳绳、羽毛球、毽球的健身运动.
小时的锻炼时间,通过调查研究,决定在七、八、九年级分别开展跳绳、羽毛球、毽球的健身运动.
国家规定初中每班的标准人数为![]() 人,七年级共有八个班,各班人数情况如下表,八年级学生人数是七年级学生人数的
人,七年级共有八个班,各班人数情况如下表,八年级学生人数是七年级学生人数的![]() 倍少
倍少![]() 人,九年级学生人数的
人,九年级学生人数的![]() 倍刚好是七、八年级学生人数的总和.(注:
倍刚好是七、八年级学生人数的总和.(注:![]() 班表示七年级一班)
班表示七年级一班)
班级 |
|
|
|
|
|
|
|
|
和每班标准 人数的差值 |
|
|
|
|
|
|
|
|
![]() 用含
用含![]() 的式子表示该中学七年级学生总数;
的式子表示该中学七年级学生总数;
![]() 学校决定按每人一根跳绳、一个毽球,两人一副羽毛球拍的标准,购买相应的体育器材以满足学生锻炼需要,其中跳绳每根
学校决定按每人一根跳绳、一个毽球,两人一副羽毛球拍的标准,购买相应的体育器材以满足学生锻炼需要,其中跳绳每根![]() 元,毽球每个
元,毽球每个![]() 元,羽毛球拍每副
元,羽毛球拍每副![]() 元.请你计算当
元.请你计算当![]() 时,学校为落实
时,学校为落实![]() 小时体育锻炼时间需购买器材的费用是多少?
小时体育锻炼时间需购买器材的费用是多少?