Question

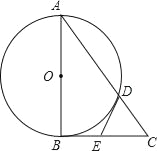
【题目】如图，一块等腰三角形钢板的底边长为，腰长为.

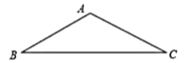
（1）求能从这块钢板上截得的最大圆的半径；

（2）用一个圆完整覆盖这块钢板，这个圆的最小半径是多少？

Answer 1

【答案】（1）cm；（2）40cm.

【解析】

（1）由于三角形ABC是等腰三角形，过A作AD⊥BC于D，那么根据勾股定理得到AD=30，又从这块钢板上截得的最大圆就是三角形的内切圆，根据内切圆的圆心的性质知道其圆心在AD上，分别连接AO、BO、CO，然后利用三角形的面积公式即可求解；

（2）由于一个圆完整覆盖这块钢板，那么这个圆是三个三角形的外接圆，设覆盖圆的半径为R，根据垂径定理和勾股定理即可求解

解：（1）如图，过A作AD⊥BC于D

∵AB=AC=50，BC=80

∴根据等腰三角形三线合一的性质及勾股定理可得

AD=30，BD=CD=40，

设最大圆半径为r，

则S△ABC=S△ABO+S△BOC+S△AOC，

∴S△ABC＝×BC×AD＝(AB+BC+CA)r

×80×30＝(50+80+50)r

解得：r=cm ；

（2）设覆盖圆的半径为R，圆心为O′，

∵△ABC是等腰三角形，过A作AD⊥BC于D，

∴BD=CD=40，AD= ，

∴O′在AD直线上，连接O′C，

在Rt△O′DC中，

由R2=402+（R-30）2，

∴R=；

若以BD长为半径为40cm，也可以覆盖，

∴最小为40cm．