题目内容
【题目】如图,在平面直角坐标系中,O为坐标原点,抛物线y= ![]() x2+2x与x轴相交于O、B,顶点为A,连接OA.
x2+2x与x轴相交于O、B,顶点为A,连接OA.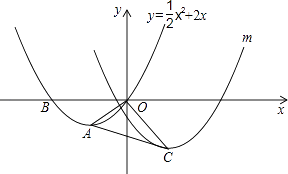
(1)求点A的坐标和∠AOB的度数;
(2)若将抛物线y= ![]() x2+2x向右平移4个单位,再向下平移2个单位,得到抛物线m,其顶点为点C.连接OC和AC,把△AOC沿OA翻折得到四边形ACOC′.试判断其形状,并说明理由;
x2+2x向右平移4个单位,再向下平移2个单位,得到抛物线m,其顶点为点C.连接OC和AC,把△AOC沿OA翻折得到四边形ACOC′.试判断其形状,并说明理由;
(3)在(2)的情况下,判断点C′是否在抛物线y= ![]() x2+2x上,请说明理由.
x2+2x上,请说明理由.
(4)若点P为x轴上的一个动点,试探究在抛物线m上是否存在点Q,使以点O、P、C、Q为顶点的四边形是平行四边形,且OC为该四边形的一条边?若存在,请直接写出点Q的坐标;若不存在,请说明理由. (参考公式:二次函数y=ax2+bx+c(a≠0)图象的顶点坐标为( ![]() ,
, ![]() ),对称轴是直线x=
),对称轴是直线x= ![]() .)
.)
【答案】
(1)
解:∵由y= ![]() x2+2x得,y=
x2+2x得,y= ![]() (x+2)2﹣2,
(x+2)2﹣2,
∴抛物线的顶点A的坐标为(﹣2,﹣2),
令 ![]() x2+2x=0,解得x1=0,x2=﹣4,
x2+2x=0,解得x1=0,x2=﹣4,
∴点B的坐标为(﹣4,0),
过点A作AD⊥x轴,垂足为D,
∴∠ADO=90°,
∴点A的坐标为(﹣2,﹣2),点D的坐标为(﹣2,0),
∴OD=AD=2,
∴∠AOB=45°;
(2)
解:四边形ACOC′为菱形.
由题意可知抛物线m的二次项系数为 ![]() ,且过顶点C的坐标是(2,﹣4),
,且过顶点C的坐标是(2,﹣4),
∴抛物线的解析式为:y= ![]() (x﹣2)2﹣4,即y=
(x﹣2)2﹣4,即y= ![]() x2﹣2x﹣2,
x2﹣2x﹣2,
过点C作CE⊥x轴,垂足为E;过点A作AF⊥CE,垂足为F,与y轴交与点H,
∴OE=2,CE=4,AF=4,CF=CE﹣EF=2,
∴OC= ![]() =2
=2 ![]() ,
,
同理,AC=2 ![]() ,OC=AC,
,OC=AC,
由翻折不变性的性质可知,OC=AC=OC′=AC′,
故四边形ACOC′为菱形.
(3)
解:如图1,点C′不在抛物线y= ![]() x2+2x上.
x2+2x上.

理由如下:
过点C′作C′G⊥x轴,垂足为G,
∵OC和OC′关于OA对称,∠AOB=∠AOH=45°,
∴∠COH=∠C′OG,
∵CE∥OH,
∴∠OCE=∠C′OG,
又∵∠CEO=∠C′GO=90°,OC=OC′,
∴△CEO≌△C′GO,
∴OG=CE=4,C′G=OE=2,
∴点C′的坐标为(﹣4,2),
把x=﹣4代入抛物线y= ![]() x2+2x得y=0,
x2+2x得y=0,
∴点C′不在抛物线y= ![]() x2+2x上;
x2+2x上;
(4)
解:
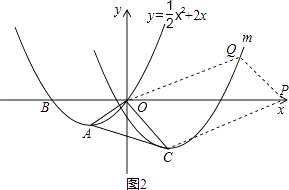
存在符合条件的点Q.
∵点P为x轴上的一个动点,点Q在抛物线m上,
∴设Q(a, ![]() (a﹣2)2﹣4),
(a﹣2)2﹣4),
∵OC为该四边形的一条边,
∴OP为对角线,
∴ ![]() =0,解得a1=6,a2=﹣2(舍去),
=0,解得a1=6,a2=﹣2(舍去),
∴点Q的坐标为(6,4).
【解析】(1)由y= ![]() x2+2x得,y=
x2+2x得,y= ![]() (x+2)2﹣2,故可得出抛物线的顶点A的坐标,令
(x+2)2﹣2,故可得出抛物线的顶点A的坐标,令 ![]() x2+2x=0得出点B的坐标过点A作AD⊥x轴,垂足为D,由∠ADO=90°可知点D的坐标,故可得出OD=AD,由此即可得出结论;(2)由题意可知抛物线m的二次项系数为
x2+2x=0得出点B的坐标过点A作AD⊥x轴,垂足为D,由∠ADO=90°可知点D的坐标,故可得出OD=AD,由此即可得出结论;(2)由题意可知抛物线m的二次项系数为 ![]() ,由此可得抛物线m的解析式过点C作CE⊥x轴,垂足为E;过点A作AF⊥CE,垂足为F,与y轴交与点H,根据勾股定理可求出OC的长,同理可得AC的长,OC=AC,由翻折不变性的性质可知,OC=AC=OC′=AC′,由此即可得出结论;(3)过点C′作C′G⊥x轴,垂足为G,由于OC和OC′关于OA对称,∠AOB=∠AOH=45°,故可得出∠COH=∠C′OG,再根据CE∥OH可知∠OCE=∠C′OG,根据全等三角形的判定定理可知△CEO≌△C′GO,故可得出点C′的坐标把x=﹣4代入抛物线y=
,由此可得抛物线m的解析式过点C作CE⊥x轴,垂足为E;过点A作AF⊥CE,垂足为F,与y轴交与点H,根据勾股定理可求出OC的长,同理可得AC的长,OC=AC,由翻折不变性的性质可知,OC=AC=OC′=AC′,由此即可得出结论;(3)过点C′作C′G⊥x轴,垂足为G,由于OC和OC′关于OA对称,∠AOB=∠AOH=45°,故可得出∠COH=∠C′OG,再根据CE∥OH可知∠OCE=∠C′OG,根据全等三角形的判定定理可知△CEO≌△C′GO,故可得出点C′的坐标把x=﹣4代入抛物线y= ![]() x2+2x进行检验即可得出结论;(4)由于点P为x轴上的一个动点,点Q在抛物线m上,故设Q(a,
x2+2x进行检验即可得出结论;(4)由于点P为x轴上的一个动点,点Q在抛物线m上,故设Q(a, ![]() (a﹣2)2﹣4),由于OC为该四边形的一条边,故OP为对角线,由于点P在x轴上,根据中点坐标的定义即可得出a的值,故可得出结论.
(a﹣2)2﹣4),由于OC为该四边形的一条边,故OP为对角线,由于点P在x轴上,根据中点坐标的定义即可得出a的值,故可得出结论.

 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案