题目内容
【题目】点B(a,5)在第二象限,点C在y轴上移动,以BC为斜边作等腰直角△BCD,我们发现直角顶点D点随着C点的移动也在一条直线上移动,这条直线的函数表达式是 .
【答案】y=﹣x+5或y=x+5
【解析】解:如图,作BF⊥y轴于F,交CD于G,连接DF. 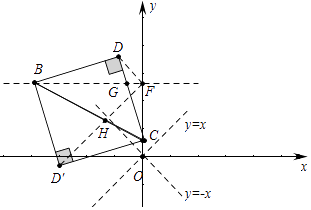
∵∠BGD=∠CGF,∠BDG=∠CFG=90°,
∴△BGD∽△CGF,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,∵∠DGF=∠BGC,
,∵∠DGF=∠BGC,
∴△DGF∽△BGC,
∴∠DFG=∠GCB=45°,
∴当点C运动时,点D在直线DF上运动,且∠DFB=45°,
易知直线DF∥直线y=﹣x,∵F(0,5),
∴直线DF的解析式为y=﹣x+5,
同法当D′在BC的下方时,点D′在Z直线FD′运动,且∠CFD′=45°,
易知D′F∥直线y=x,直线D′F的解析式为y=x+5,
所以答案是y=﹣x+5或y=x+5.
【考点精析】关于本题考查的确定一次函数的表达式,需要了解确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法才能得出正确答案.

【题目】某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分如下表:
笔 试 | 面 试 | 体 能 | |
甲 | 85 | 80 | 75 |
乙 | 80 | 90 | 73 |
丙 | 83 | 79 | 90 |
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.
(2)该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,并按60%,30%,10%的比例计入总分(不计其他因素条件),请你说明谁将被录用.
【题目】虽然近几年无锡市政府加大了太湖水治污力度,但由于大规模、高强度的经济活动和日益增加的污染负荷,使部分太湖水域水质恶化,富营养化不断加剧.为了保护水资源,我市制定一套节水的管理措施,其中对居民生活用水收费作如下规定:
月用水量(吨) | 单价(元/吨) |
不大于10吨部分 | 1.5 |
大于10吨不大于m吨部分(20≤m≤50) | 2 |
大于m吨部分 | 3 |
(1)若某用户六月份用水量为18吨,求其应缴纳的水费;
(2)记该用户六月份用水量为x吨,缴纳水费为y元,试列出y关于x的函数关系式;
(3)若该用户六月份用水量为40吨,缴纳水费y元的取值范围为70≤y≤90,试求m的取值范围.