题目内容
【题目】综合与探究
如图是一个正方形纸片![]() ,如果将正方形纸片
,如果将正方形纸片![]() 绕点
绕点![]() 逆时针旋转角度
逆时针旋转角度![]()
![]() ,得到正方形
,得到正方形![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .
.

(1)求证:![]() 平分
平分![]() ;
;
(2)直接写出线段![]() 、
、![]() 、
、![]() 之间的数量关系;
之间的数量关系;
(3)连接![]() ,
,![]() ,
,![]() ,
,![]() ,试探究在旋转过程中,四边形
,试探究在旋转过程中,四边形![]() 能否成为矩形?请说明理由.
能否成为矩形?请说明理由.
【答案】(1)见解析;(2)![]() ,理由见解析;(3)能,当点
,理由见解析;(3)能,当点![]() 为
为![]() 中点时,四边形
中点时,四边形![]() 为矩形,理由见解析
为矩形,理由见解析
【解析】
(1)根据正方形的性质和旋转的性质证明![]() ,则有
,则有![]() ,则结论可证;
,则结论可证;
(2)通过证明![]() 和
和![]() ,得出
,得出![]() ,
,![]() 则有
则有![]() ;
;
(3)当点![]() 为
为![]() 中点时,通过中点和全等三角形的性质得出
中点时,通过中点和全等三角形的性质得出![]() ,则有四边形
,则有四边形![]() 为平行四边形,又因为
为平行四边形,又因为![]() ,则可证明四边形
,则可证明四边形![]() 为矩形.
为矩形.
(1)证明:∵正方形![]() 绕点
绕点![]() 旋转得到正方形
旋转得到正方形![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,![]()
∴![]() ,
,
∴![]() ,
,
即![]() 平分
平分![]() .
.
(2)![]() ,理由如下:
,理由如下:
![]() ,
,
![]() .
.
∵正方形![]() 绕点
绕点![]() 旋转得到正方形
旋转得到正方形![]() ,
,
∴![]() ,
,![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,![]()
∴![]() ,
,
∴![]() .
.
![]() ,
,
![]() .
.
(3)能,当点![]() 为
为![]() 中点时,四边形
中点时,四边形![]() 为矩形,理由如下:
为矩形,理由如下:
如图,
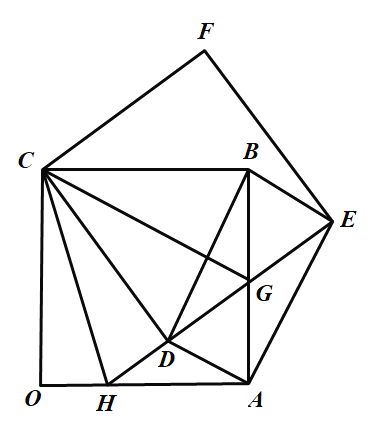
∵点![]() 为
为![]() 中点.
中点.
∴![]() .
.
∵![]() ,由(1)知
,由(1)知![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴四边形![]() 为平行四边形.
为平行四边形.
又∵![]() ,
,
∴四边形![]() 为矩形.
为矩形.

【题目】为落实立德树人根本任务,培养德智体美劳全面发展的社会主义接班人,育才学校在设立学生奖学金时规定:每学期对学生的德智体美劳五个方面进行三次综合素质评价,分别是:假期综合素质评价、期中综合素质评价、期末综合素质评价,八年级(1)班的小明和八年级(2)班的小亮两位同学同时进入一等奖学金测评,他们的三次综合素质评价成绩如下表.
假期综合素质评价成绩 | 期中综合素质评价成绩 | 期末综合素质评价成绩 | |
小明 | 96 | 91 | 92 |
小亮 | 95 | 93 | 91 |
(1)如果从三次综合素质评价成绩稳定性的角度来看,谁可以得一等奖学金?请你通过计算回答;
(2)如果假期综合素质评价成绩、期中综合素质评价成绩、期末综合素质评价成绩按![]() 的比例计入最终成绩,谁可以得一等奖学金?请你通过计算回答.
的比例计入最终成绩,谁可以得一等奖学金?请你通过计算回答.
【题目】安庆市在精准扶贫活动中,因地制宜指导农民调整种植结构,增加种植效益,2018年李大伯家在工作队的帮助下,计划种植马铃薯和蔬菜共15亩,预计每亩的投入与产出如下表:(每亩产出-每亩投入=每亩纯收入)
种类 | 投入(元) | 产出(元) |
马铃薯 | 1000 | 4500 |
蔬菜 | 1200 | 5300 |
(1)如果这15亩地的纯收入要达到54900元,需种植马铃薯和蔬菜各多少亩?
(2)如果总投入不超过16000元,则最多种植蔬菜多少亩?该情况下15亩地的纯收入是多少?