��Ŀ����
����Ŀ��������̽����
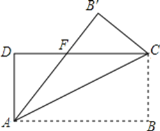
��1����ͼ1�����ı���ABCD�У���B����C��90������E�DZ�BC��һ�㣬AB��EC��BE��CD������AE��DE���жϡ�AED����״����˵�����ɣ�
��������⣩
��2����ͼ2���ڳ�����ABCD�У���P�DZ�CD��һ�㣬�ڱ�BC��AD�Ϸֱ�������E��F��ʹ�õ�F��E��P��һ������ֱ�������ε��������㣬��PE��PF����FPE��90����Ҫ����Բ����ͼ��������ͼ�ۼ�����д������
����չӦ�ã�
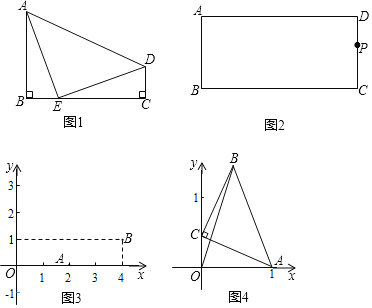
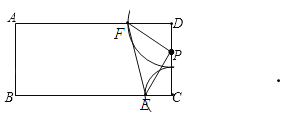
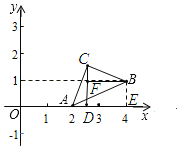
��3����ͼ3����ƽ��ֱ������ϵxOy�У���֪��A��2��0������B��4��1������C�ڵ�һ�����ڣ�����ABC�ǵ���ֱ�������Σ����C���������� ����
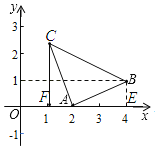
��4����ͼ4����ƽ��ֱ������ϵxOy�У���֪��A��1��0������C��y���ϵĶ��㣬�߶�CA���ŵ�C����ʱ�뷽����ת90�����߶�CB��CA��CB������BO��BA����BO+BA����Сֵ���� ����
���𰸡���1����AED�ǵ���ֱ�������Σ���2�������������3����1��2������3��3������![]() ��
��![]() ������4��
������4��![]()
��������
��1��֤����ABE�ա�ECD ��SAS����������⣻
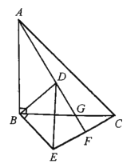
��2����ͼ���Ե�DΪԲ��CP��Ϊ�뾶������AD�ڵ�F���Ե�CΪԲ�ģ�DP��Ϊ�뾶������BE�ڵ�E������EF��EP��FP����E��F��Ϊ����
��3���֡�CAB=90������ABC=90������ACB=90�������������⼴�ɣ�
��4�����B��m��1+m������BO+BA=![]() ��BO+BA��ֵ�൱�����P��m��m������M��1��-1���͵�N��0��-1������Сֵ��������⣮
��BO+BA��ֵ�൱�����P��m��m������M��1��-1���͵�N��0��-1������Сֵ��������⣮
�⣺��1����AED�ǵ���ֱ�������Σ�
֤�������ڡ�ABE�͡�ECD�У�
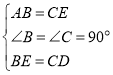 ,
,
���ABE�ա�ECD ��SAS��
��AE��DE����AEB����EDC��
����Rt��EDC����C��90����
���EDC+��DEC��90����
���AEB+��DEC��90����
�ߡ�AEB+��DEC+��AED��180����
���AED��90����
���AED�ǵ���ֱ�������Σ�
��2����ͼ���Ե�DΪԲ��CP��Ϊ�뾶������AD�ڵ�F���Ե�CΪԲ�ģ�DP��Ϊ�뾶������BE�ڵ�E������EF��EP��FP��
���E��F������
��3����ͼ������CAB��90����CA��ABʱ������C��CF��AO�ڵ�F������B��BE��AO�ڵ�E��
�ߵ�A��2��0������B��4��1����
��BE��1��OA��2��OE��4����AE��2��
�ߡ�CAB��90����BE��AO��
���CAF+��BAE��90������BAE+��ABE��90����
���CAF����ABE����AC��AB����AFC����AEB��90����
���ACF�ա�BAE��AAS��
��CF��AE��2��AF��BE��1��
��OF��OA��AF��1��
���C������1��2��
��ͼ������ABC��90����AB��BCʱ������B��BE��OA������C��CF��BE
�ߡ�ABC��90����BE��OA��
���ABE+��CBF��90������ABE+��BAE��90����
���BAE����CBF����BC��AB����AEB����CFB��90��
���BCF�ա�ABE��AAS��
��BE��CF��1��AE��BF��2����EF��3
���C������3��3��
��ͼ������ACB��90����CA��BCʱ������C��CD��OA�ڵ�D������B��BF��CD�ڵ�F��
�ߡ�ACD+��BCF��90������ACD+��CAD��90����
���BCF����CAD����AC��BC����CDA����CFB��
���ACD�ա�CBF��AAS��
��CF��AD��BF��CD��DE��
��AD+DE��AE��2
��2��AD+CD��AD+CF+DF��2AD+1
��DA��![]() ��
��
��CD��![]() ��OD��
��OD��![]() ��
��
���C���꣨![]() ��
��![]() ��
��
������������C��������1��2������3��3������![]() ��
��![]() ��
��
�ʴ�Ϊ����1��2������3��3������![]() ��
��![]() ��
��
��4����ͼ��BH��OH��H��
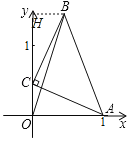
���C��������0��m����
�ɣ�1��֪��OC��HB��m��OA��HC��1��
���B��m��1+m����
��BO+BA��![]() ��
��
BO+BA��ֵ���൱�����P��m��m������M��1����1���͵�N��0����1������Сֵ��
�൱����ֱ��y��x��Ѱ��һ��P��m��m����ʹ�õ�P��M��0����1������N��1����1���ľ������С��
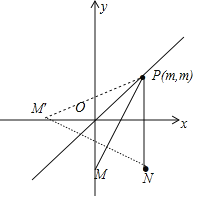
��M����ֱ��y��x�ĶԳƵ�M������1��0����
��֪PM+PN��PM��+PN��NM����
M��N��![]() ��
��
�ʣ�BO+BA����СֵΪ![]() ��
��

 �»����ܶ�Ա��ϵ�д�
�»����ܶ�Ա��ϵ�д� ����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�
����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�����Ŀ�����˹�˾�涨�ÿͿ����Я��һ��������������������������涨ʱ���踶�������y��Ԫ������������x��kg����һ�κ������Ҳ��ֶ�Ӧ��ϵ�����ʾ��
x��kg�� | �� | 30 | 40 | 50 | �� |
y��Ԫ�� | �� | 4 | 6 | 8 | �� |
��1����y����x�ĺ�������ʽ��
��2�����ÿ��������Я�������������
��3���������2��y��7��Ԫ��ʱ����Я�����������x��kg����ȡֵ��Χ���� ����