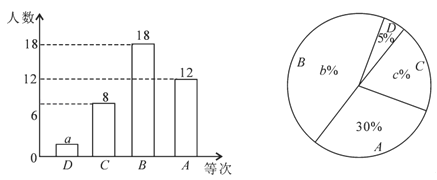
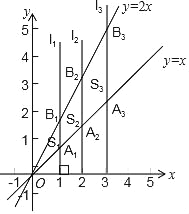
��Ŀ����
����Ŀ���Ķ����ϣ�С����������һ�����⣺��ͼ1������ABC�У�AB��AC������B������BE����DΪ����BE�ϵĵ㣬����AD��CD���ҡ�BDC����BAC����֤��ADƽ�֡�CDE��С������۲�ͼ�Σ��ַ���һ����ȵĽǣ�������ȵ�һ�ԽǺ�һ�Աߣ�����A��˫��ֱ������ȫ�������Σ���ͼ2���Ӷ�����������
��1�������Ķ����ϣ�֤��ADƽ�֡�CDE��
��ѧ����֪ʶ��ο�С���ķ����������������⣺
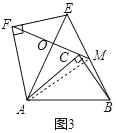
��2����ͼ3����Rt��ABC�У���ACB��90������A��������Rt��ABC�Ƶ�A��ʱ����ת�õ���AEF����C�Ķ�Ӧ��Ϊ��F��������BE��FC���ӳ�FC��B�ڵ�M��
���ҳ�ͼ�����BCM��ȵĽǣ�������֤����
�ڲ����߶�CF��BM֮���������ϵ���ú�����ʽ�ӱ�ʾ������֤����IJ��룮
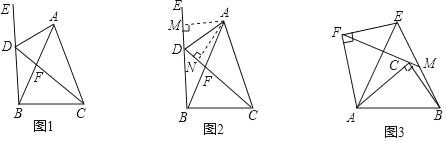
���𰸡���1������������2���١�BCM����EFM�����ɼ��������ڲ��룺FC��2BMcos�������ɼ�������
��������
��1����ͼ2�У���AM��BE��M��AN��CD��N������ȫ�������ε�����֤��AM��AN���ɣ�
��2���ٽ��ۣ���BCM����EFM�����õȽǵ�������֤�����ɣ��ڲ��룺FC��2BMcos������ͼ3�У�����AM����AE��FM�ڵ�O������֤��AM��BE�����������������ε����ʼ���֤����
��1��֤������ͼ2�У���AM��BE��M��AN��CD��N��
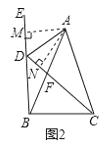
�ߡ�BDF����CAF����DFB����AFC��
���DBF����ACF��
�ߡ�AMB����ANC��90������ABM����ACN��AB��AC��
���ABM�ա�ACN��AAS����
��AM��AN����AM��DM��AN��DN��
��ADƽ�֡�CDE��
��2���⣺�ٽ��ۣ���BCM����EFM��
���ɣ���ͼ3�У���AC��AF��
���ACF����AFC��
�ߡ�ACB����AFE��90����
���ACF+��BCM��90������AFC+��MFE��90����
���BCM����EFM��
�۲��룺FC��2BMcos����
���ɣ���ͼ3�У�����AM����AE��FM�ڵ�O��
�ߡ�CAB����EAF������
���BAE����CAF��
��AC��AF��AE��AB��
���AFC����ACF����AEB����ABE��
�ߡ�AOF����MOE��
���AOF�ס�MOE��
��![]() ��
��
��![]() ���ߡ�EOF����AOM��
���ߡ�EOF����AOM��
���EOF�ס�MOA��
���OAM����EFO��
�ߡ�OFO���ϡ�OEM����OFA+��EFO��90����
���OAM+��OEM��90����
���AME��90����
��AE��AB��
��BM��![]() BE��
BE��
�ߡ�FAC�ס�EAB��
��![]() ��cos����
��cos����
��![]() ��cos����
��cos����
��FC��2BMcos����

 �ۺ��Բ�ϵ�д�
�ۺ��Բ�ϵ�д�����Ŀ����֪���κ���y��ax2+bx+c��a��0��������y���Ա���x�IJ��ֶ�Ӧֵ���±���
x | ���� | ��1 | 0 | 1 | 4 | ���� |
y | ���� | 12 | 6 | 2 | 2 | ���� |
��1������κ����Ľ���ʽ��
��2��ֱ��д������ʽax2+bx+c��2��0�Ľ⼯���� ����