Question

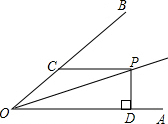如图，OP平分∠BOA，∠BOA=45°，PC∥OA，PD⊥OA．若PC=6，则PD等于（　　）

• A．6
• B．3

  2

• C．2

  3

• D．3

Answer 1

分析：根据角平分线的性质，角平分线上的点到两角的距离相等，因而过P作PE⊥OB于点E，则PD=PE，因为PC∥OA，得角相等，而OP平分∠BOA，得∴∠ECP=∠COP+∠OPC=45°根据三角形的外角的性质得到答案．

解答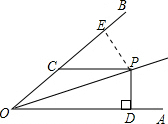：解：过P作PE⊥OB于点E，则PD=PE，
∵PC∥OA，∠BOA=45°，
∴∠ECP=∠AOB=45°．
在Rt△ECP中，PE=

2

2

PC=

2

2

×6=3

2

，
∴PD=PE=3

2

．
故选B．

点评：本题主要考查了角平分线的性质，角平分线上的点到角的两边距离相等．