��Ŀ����
��2012•�γǶ�ģ����ͼ����ƽ��ֱ������ϵ�У���ֱ֪��AB��y=-
x+3�ֱ���x�ᡢy��ֱ��ڵ�A����B������P��Q�ֱ��O��Aͬʱ���������е�P��ÿ��1����λ���ȵ��ٶ���OA������A�������˶�������A���������ԭ�ٶ���AO����Q��ÿ��1����λ���ȵ��ٶȴ�A���������A-B-O������O�������˶�������Q�����Oʱ��P��Q����ͬʱֹͣ�˶������˶�ʱ��Ϊt���룩��
��1�����A���B�����ꣻ
��2����ͼ1����ijһʱ�̽���APQ��PQ���ۣ�ʹ��Aǡ������AB�ߵĵ�C�������ʱ��APQ�������
��3����DΪy����һ�㣬�ڵ�P��O��A�˶��Ĺ����У��Ƿ����ijһʱ�̣�ʹ���ı���PQBDΪ�������Σ������ڣ����t��ֵ��D�����ꣻ�������ڣ���˵�����ɣ�
��4����ͼ2����P��Q�����˶������У��߶�PQ�Ĵ�ֱƽ����EF��PQ�ڵ�E��������QB-BO-OP�ڵ�F���ʣ��Ƿ����ijһʱ��t��ʹEFǡ�þ���ԭ��O�������ڣ���������з���������t��ֵ���������ڣ���˵�����ɣ�
| 3 | 4 |
��1�����A���B�����ꣻ
��2����ͼ1����ijһʱ�̽���APQ��PQ���ۣ�ʹ��Aǡ������AB�ߵĵ�C�������ʱ��APQ�������
��3����DΪy����һ�㣬�ڵ�P��O��A�˶��Ĺ����У��Ƿ����ijһʱ�̣�ʹ���ı���PQBDΪ�������Σ������ڣ����t��ֵ��D�����ꣻ�������ڣ���˵�����ɣ�
��4����ͼ2����P��Q�����˶������У��߶�PQ�Ĵ�ֱƽ����EF��PQ�ڵ�E��������QB-BO-OP�ڵ�F���ʣ��Ƿ����ijһʱ��t��ʹEFǡ�þ���ԭ��O�������ڣ���������з���������t��ֵ���������ڣ���˵�����ɣ�

��������1���ֱ����ֱ��AB��������Ľ������꼴�����A����B������ꣻ
��2��������APQ��PQ���ۣ�ʹ��Aǡ������AB�ߵĵ�C��ʱ����AQP=90�㣬Ȼ��������������������߶�AQ���߶�PQ�ij��������������APQ�������
��3������PD��BQ��������PQBD�ǵ������Σ���D��P�ֱַ���DM��AB��M��PN��AB��N���������PNMD������BM=QN����PD��BQ����
=
���Ӷ����MB��ֵ����ֱ��������APN�и���AP���QN��ֵ��Ȼ����BM=QN�����t�����Ե�E�������ӭ�ж����ˣ�
����PQ��BD�����������PQBD��BQ=EP��PQ��OA��P�㣮��OP+AP=OA���tֵ��
��4���ٵ�P��O��A�˶�ʱ��OQ=OP=AQ=t�����б߽ǹ�ϵ���BQ=AQ=
AD�����tֵ���ڢڵ�P��A��O�˶�ʱ��OQ=OP=8-t����Rt��OGQ�У����ù��ɶ�����OQ2=QG2+OG2���г�����t�ķ��̣��ⷽ�̼��ɣ�
��2��������APQ��PQ���ۣ�ʹ��Aǡ������AB�ߵĵ�C��ʱ����AQP=90�㣬Ȼ��������������������߶�AQ���߶�PQ�ij��������������APQ�������
��3������PD��BQ��������PQBD�ǵ������Σ���D��P�ֱַ���DM��AB��M��PN��AB��N���������PNMD������BM=QN����PD��BQ����
| OE |
| OB |
| OP |
| OA |
����PQ��BD�����������PQBD��BQ=EP��PQ��OA��P�㣮��OP+AP=OA���tֵ��
��4���ٵ�P��O��A�˶�ʱ��OQ=OP=AQ=t�����б߽ǹ�ϵ���BQ=AQ=
| 1 |
| 2 |
����⣺��1����y=-
x+3=0�����x=4��
���A��������4��0����
��x=0����y=-
��0+3=3��
���B����������0��3����
��2��������֪����ʱ��APQ�ա�DPQ����AQP=90�㣬
��ʱ��AQP�ס�AOB��AQ=t��AP=4-t
��
=
=
����
=
=
��ã�AQ=t=
��QP=
��
��S��APQ=
AQ•PQ=
��
��
=
��
��3�����ڣ��������������
����PE��BQ�����������PQBE��PQ=BE
��E��P�ֱַ���EM��AB��M��PN��AB��N��
����BM=QN����PE��BQ��
��
=
��
��BM=
��3-
t����
�֡�AP=4-t��
��AN=
��4-t����
��QN=
��4-t��-t��
��BM=QN����
��3-
t��=
��4-t��-t
��t=
��
��E��0��
����
����PQ��BE�����������PQBE��
BQ=EP��PQ��OA��P��
������֪AP=
AQ=
t
��OP+AP=OA��
��t+
t=4
��t=
��
��OE=
��
���E��0��-
��
�ɢ٢ڵ�E������Ϊ��0��
����0��-
����
��4������OQ��������Q��QG��y��y��G��
�ٵ�P��O��A�˶�ʱ��OQ=OP=AQ=t��
�ɵá�QOA=��QAO���QOB=��QBO
��OQ=BQ=t
��BQ=AQ=
AB
��t=
����Q�ɵ�B���O�����˶�����5��t��8ʱ����OPQʼ���ǵ���ֱ�������Σ���ô�߶�PQ�Ĵ�ֱƽ����EF�ض�������ԭ��O������5��t��8ʱҲ����������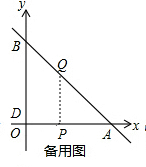
���Ϣ١��ڡ������������з���������t��ֵ��t=
5��t��8��
������OQ��������Q��QG��y��y��G��
��P��A��O�˶�ʱ��OQ=OP=8-t
BQ=5-t��QG=
��5-t����OG=3-
��5-t��
��Rt��OGQ��OQ2=QG2+OG2
����8-t��2=[
��5-t��]2+[3-
��5-t��]2
��t=5
| 3 |
| 4 |
���A��������4��0����
��x=0����y=-
| 3 |
| 4 |
���B����������0��3����
��2��������֪����ʱ��APQ�ա�DPQ����AQP=90�㣬
��ʱ��AQP�ס�AOB��AQ=t��AP=4-t
��
| AQ |
| AO |
| AP |
| AB |
| QP |
| OB |
����
| t |
| 4 |
| 4-t |
| 5 |
| QP |
| 3 |
��ã�AQ=t=
| 16 |
| 9 |
| 4 |
| 3 |
��S��APQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 16 |
| 9 |
| 4 |
| 3 |
| 32 |
| 27 |
��3�����ڣ��������������
����PE��BQ�����������PQBE��PQ=BE
��E��P�ֱַ���EM��AB��M��PN��AB��N��
����BM=QN����PE��BQ��
��
| OE |
| OB |
| OP |
| OA |
��BM=
| 3 |
| 5 |
| 3 |
| 4 |
�֡�AP=4-t��
��AN=
| 4 |
| 5 |
��QN=
| 4 |
| 5 |
��BM=QN����
| 3 |
| 5 |
| 3 |
| 4 |
| 4 |
| 5 |
��t=
| 28 |
| 27 |
��E��0��
| 7 |
| 9 |
����PQ��BE�����������PQBE��
BQ=EP��PQ��OA��P��
������֪AP=
| 4 |
| 5 |
| 4 |
| 5 |
��OP+AP=OA��
��t+
| 4 |
| 5 |
��t=
| 20 |
| 9 |
��OE=
| 5 |
| 3 |
���E��0��-
| 5 |
| 3 |
�ɢ٢ڵ�E������Ϊ��0��
| 7 |
| 9 |
| 5 |
| 3 |
��4������OQ��������Q��QG��y��y��G��
�ٵ�P��O��A�˶�ʱ��OQ=OP=AQ=t��
�ɵá�QOA=��QAO���QOB=��QBO
��OQ=BQ=t
��BQ=AQ=
| 1 |
| 2 |
��t=
| 5 |
| 2 |
����Q�ɵ�B���O�����˶�����5��t��8ʱ����OPQʼ���ǵ���ֱ�������Σ���ô�߶�PQ�Ĵ�ֱƽ����EF�ض�������ԭ��O������5��t��8ʱҲ����������

���Ϣ١��ڡ������������з���������t��ֵ��t=
| 5 |
| 2 |
������OQ��������Q��QG��y��y��G��
��P��A��O�˶�ʱ��OQ=OP=8-t
BQ=5-t��QG=
| 4 |
| 5 |
| 3 |
| 5 |
��Rt��OGQ��OQ2=QG2+OG2
����8-t��2=[
| 4 |
| 5 |
| 3 |
| 5 |
��t=5
������������Ҫ������һ�κ�����Ӧ�ã����������ε������Լ����κ�����֪ʶ����ۺ�Ӧ�ã�Ū������߶εĴ�С�ͱ�����ϵ�ǽ���Ĺؼ���

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
 ��2012•�γǶ�ģ����ͼ�����뾶Ϊ2��Բ��ֽƬ�۵���Բ��ǡ�þ���Բ��O�����ۺ�AB�ij�Ϊ
��2012•�γǶ�ģ����ͼ�����뾶Ϊ2��Բ��ֽƬ�۵���Բ��ǡ�þ���Բ��O�����ۺ�AB�ij�Ϊ