��Ŀ����
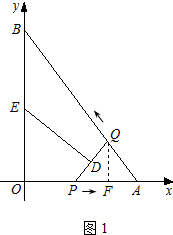
��ͼ����ƽ��ֱ������ϵxOy�У�ֱ��AB��x�ύ�ڵ�A����y�ύ�ڵ�B����OA=3��AB=5����P�ӵ�O������OA��ÿ��1����λ�����ٶ����A�����˶��������A��������ԭ�����ٶ���AO���أ���Q�ӵ�A������AB��ÿ��1����λ�����ٶ����B�����˶��������� P��Q���˶���DE���ִ�ֱƽ��PQ���ҽ�PQ�ڵ�D��������QB-BO-OP�ڵ�E����P��Qͬʱ����������Q�����Bʱֹͣ�˶�����PҲ��ֹ֮ͣ�����P��Q�˶���ʱ����t�루t��0����
P��Q���˶���DE���ִ�ֱƽ��PQ���ҽ�PQ�ڵ�D��������QB-BO-OP�ڵ�E����P��Qͬʱ����������Q�����Bʱֹͣ�˶�����PҲ��ֹ֮ͣ�����P��Q�˶���ʱ����t�루t��0������1����ֱ��AB�Ľ���ʽ��
��2���ڵ�P��O��A�˶��Ĺ����У����APQ�����S��t֮��ĺ�����ϵʽ������д��t��ȡֵ��Χ����
��3���ڵ�E��B��O�˶��Ĺ����У�����������⣺
���ı���QBED�ܷ��Ϊֱ�����Σ����ܣ������t��ֵ�������ܣ���˵�����ɣ�
�ڵ�DE������Oʱ������ֱ��д��t��ֵ��
��������1����������Rt��AOB�У�OA=3��AB=5�����OB��ֵ��Ȼ�����ô���ϵ�����������һ�κ����Ľ���ʽ��
��2������Q��QF��AO�ڵ�F���ɡ�AQF�ס�ABO���������������εĶ�Ӧ�߳ɱ����������ڷ��̼������QF�ij���Ȼ����á�APQ�����S��t֮��ĺ�����ϵʽ��
��3���ٷֱ��DE��QB��PQ��BOȥ���������������������ε����ʣ��������t��ֵ��
�ڸ��������֪��OP=OQʱ�����з��̼������t��ֵ��
��2������Q��QF��AO�ڵ�F���ɡ�AQF�ס�ABO���������������εĶ�Ӧ�߳ɱ����������ڷ��̼������QF�ij���Ȼ����á�APQ�����S��t֮��ĺ�����ϵʽ��
��3���ٷֱ��DE��QB��PQ��BOȥ���������������������ε����ʣ��������t��ֵ��
�ڸ��������֪��OP=OQʱ�����з��̼������t��ֵ��
��� �⣺��1����Rt��AOB�У�OA=3��AB=5���ɹ��ɶ�����OB=
�⣺��1����Rt��AOB�У�OA=3��AB=5���ɹ��ɶ�����OB=
=4��
��A��3��0����B��0��4����
��ֱ��AB�Ľ���ʽΪy=kx+b��
��
���
��ֱ��AB�Ľ���ʽΪy=-
x+4��
��2����ͼ1������Q��QF��AO�ڵ�F��
��AQ=OP=t����AP=3-t��
�ɡ�AQF�ס�ABO����
=
��
��
=
��
��QF=
t��
��S=
��3-t��•
t��
��S=-
t2+
t��
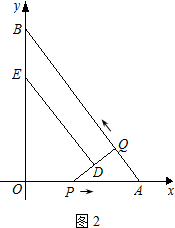
��3���ı���QBED�ܳ�Ϊֱ�����Σ�
����ͼ2����DE��QBʱ��
��DE��PQ��
��PQ��QB���ı���QBED��ֱ�����Σ�
��ʱ��AQP=90�㣮
�ɡ�APQ�ס�ABO����
=
��
��
=
��
���t=
��
��ͼ3����PQ��BOʱ��
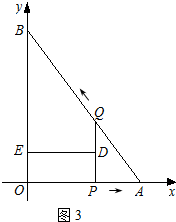 ��DE��PQ��
��DE��PQ��
��DE��BO���ı���QBED��ֱ�����Σ�
��ʱ��APQ=90�㣮
�ɡ�AQP�ס�ABO����
=
��
��
=
��
3t=5��3-t����
3t=15-5t��
8t=15��
���t=
��
����P��A��0�˶��Ĺ����л���������������������ȥ��
�ڵ�DE������Oʱ��
��DE��ֱƽ��PQ��
��EP=EQ=t��
����P��Q��ͬ��ʱ����ٶȣ�
��AQ=EQ=EP=t��
���AEQ=��EAQ��
�ߡ�AEQ+��BEQ=90�㣬��EAQ+��EBQ=90�㣬
���BEQ=��EBQ��
��BQ=EQ��
��EQ=AQ=BQ=
AB
����t=
��
��P��A��O�˶�ʱ��
����Q��QF��OB��F��
EP=6-t��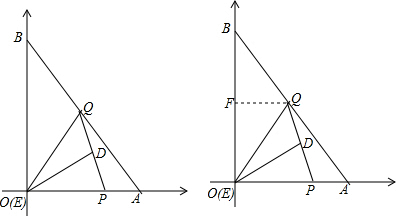
��EQ=EP=6-t��
AQ=t��BQ=5-t��
��FQ=
��5-t��=3-
t��BF=
��5-t��=4-
t��
��EF=4-BF=
t��
��EF2+FQ2=EQ2��
����3-
t��2+��
t��2=��6-t��2��
��ã�t=
��
�൱DE������Oʱ��t=
��
��
 �⣺��1����Rt��AOB�У�OA=3��AB=5���ɹ��ɶ�����OB=
�⣺��1����Rt��AOB�У�OA=3��AB=5���ɹ��ɶ�����OB=| AB2-OA2 |
��A��3��0����B��0��4����
��ֱ��AB�Ľ���ʽΪy=kx+b��
��
|
|
��ֱ��AB�Ľ���ʽΪy=-
| 4 |
| 3 |
��2����ͼ1������Q��QF��AO�ڵ�F��
��AQ=OP=t����AP=3-t��
�ɡ�AQF�ס�ABO����
| QF |
| BO |
| AQ |
| AB |
��
| QF |
| 4 |
| t |
| 5 |
��QF=
| 4 |
| 5 |
��S=
| 1 |
| 2 |
| 4 |
| 5 |
��S=-
| 2 |
| 5 |
| 6 |
| 5 |

��3���ı���QBED�ܳ�Ϊֱ�����Σ�
����ͼ2����DE��QBʱ��
��DE��PQ��
��PQ��QB���ı���QBED��ֱ�����Σ�
��ʱ��AQP=90�㣮
�ɡ�APQ�ס�ABO����
| AQ |
| AO |
| AP |
| AB |
��
| t |
| 3 |
| 3-t |
| 5 |
���t=
| 9 |
| 8 |
��ͼ3����PQ��BOʱ��
 ��DE��PQ��
��DE��PQ����DE��BO���ı���QBED��ֱ�����Σ�
��ʱ��APQ=90�㣮
�ɡ�AQP�ס�ABO����
| AQ |
| AB |
| AP |
| AO |
��
| t |
| 5 |
| 3-t |
| 3 |
3t=5��3-t����
3t=15-5t��
8t=15��
���t=
| 15 |
| 8 |
����P��A��0�˶��Ĺ����л���������������������ȥ��
�ڵ�DE������Oʱ��
��DE��ֱƽ��PQ��
��EP=EQ=t��
����P��Q��ͬ��ʱ����ٶȣ�
��AQ=EQ=EP=t��
���AEQ=��EAQ��
�ߡ�AEQ+��BEQ=90�㣬��EAQ+��EBQ=90�㣬
���BEQ=��EBQ��
��BQ=EQ��
��EQ=AQ=BQ=
| 1 |
| 2 |
����t=
| 5 |
| 2 |
��P��A��O�˶�ʱ��
����Q��QF��OB��F��
EP=6-t��

��EQ=EP=6-t��
AQ=t��BQ=5-t��
��FQ=
| 3 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
��EF=4-BF=
| 4 |
| 5 |
��EF2+FQ2=EQ2��
����3-
| 3 |
| 5 |
| 4 |
| 5 |
��ã�t=
| 45 |
| 14 |
�൱DE������Oʱ��t=
| 5 |
| 2 |
| 45 |
| 14 |
���������⿼���˴���ϵ������һ�κ����Ľ���ʽ�����������ε��ж������ʵ�֪ʶ��Ӧ�ã������ۺ��Խ�ǿ��ע�����ν���뷽��˼���Ӧ�ã�

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
 ��ͼ����ƽ��ֱ�������У��ı���OABC�ǵ������Σ�CB��OA��OA=7��AB=4����COA=60�㣬��PΪx���ϵ�һ�����㣬���ǵ�P�����0����A�غϣ�����CP��D�����߶�AB��һ�㣬����PD��
��ͼ����ƽ��ֱ�������У��ı���OABC�ǵ������Σ�CB��OA��OA=7��AB=4����COA=60�㣬��PΪx���ϵ�һ�����㣬���ǵ�P�����0����A�غϣ�����CP��D�����߶�AB��һ�㣬����PD�� ��2012•�山��һģ����ͼ����ƽ��ֱ������xoy�У�������ԭ��OΪԲ�ģ�3Ϊ�뾶��Բ���Ӵ�Բ�ڣ������߽磩�����������㣨�ᡢ�������Ϊ������������ѡȡһ���㣬��ᡢ������֮��Ϊ0�ĸ�����
��2012•�山��һģ����ͼ����ƽ��ֱ������xoy�У�������ԭ��OΪԲ�ģ�3Ϊ�뾶��Բ���Ӵ�Բ�ڣ������߽磩�����������㣨�ᡢ�������Ϊ������������ѡȡһ���㣬��ᡢ������֮��Ϊ0�ĸ����� ��ͼ����ƽ��ֱ�������У���������ABCD���µ���x���ϣ���B������Ϊ��4��0����D������Ϊ��0��3������AC��Ϊ
��ͼ����ƽ��ֱ�������У���������ABCD���µ���x���ϣ���B������Ϊ��4��0����D������Ϊ��0��3������AC��Ϊ ��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ���������
��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ��������� ��COA=45�㣬����P�ӵ�O������������OABC�ı����˶���·��ΪO��A��B��C�������Cʱֹͣ����ֱ��CP��
��COA=45�㣬����P�ӵ�O������������OABC�ı����˶���·��ΪO��A��B��C�������Cʱֹͣ����ֱ��CP��