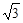题目内容
如图,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF,求证:AC=BF.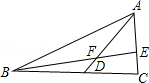

有两种解法:
①延长AD至点M,使MD=FD,连接MC,则可证△BDF≌△CDM(SAS),可得MC=BF,∠M=∠BFM,再得∠M=∠MAC,得AC=MC=BF.
②延长AD至点M,使DM=AD,连接BM,可证△ADC≌△MDB(SAS),方法与①相同.
①延长AD至点M,使MD=FD,连接MC,则可证△BDF≌△CDM(SAS),可得MC=BF,∠M=∠BFM,再得∠M=∠MAC,得AC=MC=BF.
②延长AD至点M,使DM=AD,连接BM,可证△ADC≌△MDB(SAS),方法与①相同.
试题分析:有两种解法:
①延长AD至点M,使MD=FD,连接MC,则可证△BDF≌△CDM(SAS),可得MC=BF,∠M=∠BFM,再得∠M=∠MAC,得AC=MC=BF.
②延长AD至点M,使DM=AD,连接BM,可证△ADC≌△MDB(SAS),方法与①相同.
证明:方法一:延长AD至点M,使MD=FD,连接MC,
在△BDF和△CDM中,
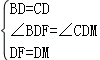
∴△BDF≌△CDM(SAS).
∴MC=BF,∠M=∠BFM.
∵EA=EF,
∴∠EAF=∠EFA,
∵∠AFE=∠BFM,
∴∠M=∠MAC,
∴AC=MC,
∴BF=AC;
方法二:延长AD至点M,使DM=AD,连接BM,
在△ADC和△MDB中,
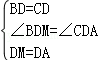 ,
,∴△ADC≌△MDB(SAS),
∴∠M=∠MAC,BM=AC,
∵EA=EF,
∴∠CAM=∠AFE,而∠AFE=∠BFM,
∴∠M=∠BFM,
∴BM=BF,
∴BF=AC.
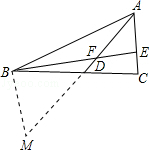
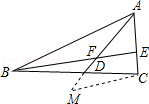
点评:本题考查了三角形全等的判定及性质、等腰三角形的性质.其中普通两个三角形全等共有四个定理,即AAS、ASA、SAS、SSS,解决此题的关键是作出巧妙的辅助线:倍长中线.

练习册系列答案
相关题目




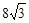 ,∠B=30°, 则DE的长是( )
,∠B=30°, 则DE的长是( )