题目内容
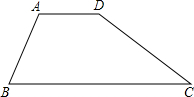 已知:如图,梯形ABCD中,AD∥BC,AB=CD=
已知:如图,梯形ABCD中,AD∥BC,AB=CD=| 2 |
分析:由于动点E在折线BA-AD-DC上移动,所以此题应分别画出对应的三种情况进行讨论计算.作等腰梯形的两条高,根据已知的线段和已知的角求得该梯形的高是1,下底是3.再进一步根据BP=x进行表示各个图形的面积.
解答: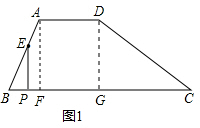 解:作AF⊥BC于F,DG⊥BC于G.
解:作AF⊥BC于F,DG⊥BC于G.
在Rt△ABF中,AB=CD=
,∠B=45°,
∴AF=BF=1,同理,DG=CG=1,则BC=1+1+1=3.
则梯形的面积=
(1+3)×1=2.
当E分别在折线BA、AD、DC上移动时:
(1)如图1,当点E在AB上时,则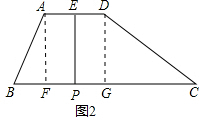 △BEP的面积是
△BEP的面积是
,五边形AEPCD的面积=2-
.
(2)如图2,当点E在AD上时,则四边形ABPE的面积=
(x+x-1)×1=x-
;
四边形CDEP的面积=2-(x-
)=
-x.
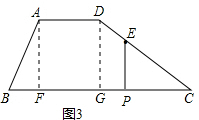
(3)如图3,当点E在CD上时,△CEP的面积=
(3-x)2=
x2-3x+
;
五边形ABPED的面积=2-(
x2-3x+
)=-
x2+3x-
.
 解:作AF⊥BC于F,DG⊥BC于G.
解:作AF⊥BC于F,DG⊥BC于G.在Rt△ABF中,AB=CD=
| 2 |
∴AF=BF=1,同理,DG=CG=1,则BC=1+1+1=3.
则梯形的面积=
| 1 |
| 2 |
当E分别在折线BA、AD、DC上移动时:
(1)如图1,当点E在AB上时,则
 △BEP的面积是
△BEP的面积是| x2 |
| 2 |
| x2 |
| 2 |
(2)如图2,当点E在AD上时,则四边形ABPE的面积=
| 1 |
| 2 |
| 1 |
| 2 |
四边形CDEP的面积=2-(x-
| 1 |
| 2 |
| 5 |
| 2 |
(3)如图3,当点E在CD上时,△CEP的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |

五边形ABPED的面积=2-(
| 1 |
| 2 |
| 9 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
点评:此题要首先能够根据梯形中的已知条件求得梯形的下底和高,然后结合三种情况的图进行分析计算,尤其要注意其中的等腰直角三角形.

练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 9、已知:如图,梯形ABCD中,AD∥BC,AB=CD,对角线AC与BD相交于点O,则图中全等三角形共有( )
9、已知:如图,梯形ABCD中,AD∥BC,AB=CD,对角线AC与BD相交于点O,则图中全等三角形共有( )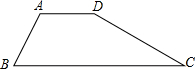 已知:如图,梯形ABCD中,AD∥BC,∠DAB=120°,tanC=
已知:如图,梯形ABCD中,AD∥BC,∠DAB=120°,tanC=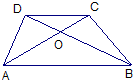 8、已知,如图,梯形ABCD中,AB∥CD,△COD与△AOB的周长比为1:2,则CD:AB=
8、已知,如图,梯形ABCD中,AB∥CD,△COD与△AOB的周长比为1:2,则CD:AB= 已知:如图,梯形ABCD中,AB∥CD,AD=BC,对角线AC、BD交于M,AB=2,CD=4,∠CMD=90°,求:BD的长.
已知:如图,梯形ABCD中,AB∥CD,AD=BC,对角线AC、BD交于M,AB=2,CD=4,∠CMD=90°,求:BD的长.