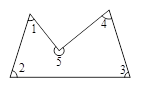题目内容
已知△ABC是等边三角形,点D、F分别在边BC、AC上,且DF∥AB,过点A平行于BC的直线与DF的延长线交于点E,连结CE、BF.
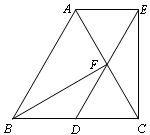
(1)求证:△ABF≌△ACE;
(2)若D是BC的中点,判断△DCE的形状,并说明理由.

(1)求证:△ABF≌△ACE;
(2)若D是BC的中点,判断△DCE的形状,并说明理由.
(1)根据等边三角形的性质可得AB=AC,∠BAC=∠ACB=60°,再根据平行线的性质可得∠EFA=∠BAC=60°,∠CAE=∠ACB=60°,即可得到△EAF是等边三角形,从而证得结论;(2)直角三角形
试题分析:(1)根据等边三角形的性质可得AB=AC,∠BAC=∠ACB=60°,再根据平行线的性质可得∠EFA=∠BAC=60°,∠CAE=∠ACB=60°,即可得到△EAF是等边三角形,从而证得结论;
(2)连接AD.先根据平行四边形的定义证得四边形ABDE是平行四边形,即得AE=BD,再根据中点的性质可得BD=DC,再结合AE∥DC可得四边形ADCE是平行四边形,再根据等腰三角形的性质证明即可.
(1)∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠ACB=60°.
∵DE∥AB,AE∥BD,
∴∠EFA=∠BAC=60°,∠CAE=∠ACB=60°.
∴△EAF是等边三角形.
∴AF=AE.
在△ABF和△ACE中,
∵AB=AC,∠BAF=∠CAE=60°,AF=AE,
∴△ABF≌△ACE.
(2)△DCE是直角三角形,∠DCE=90°
理由:连接AD.

∵DE∥AB,AE∥BD,
∴四边形ABDE是平行四边形.
∴AE=BD.
∵D是BC中点,
∴BD=DC.
∴AE=DC.
∵AE∥DC,
∴四边形ADCE是平行四边形.
∵AB=AC,D是BC中点,
∴AD⊥DC.
∴四边形ADCE是矩形.
∴△DCE是直角三角形,∠DCE=90°.
点评:本题知识点较多,综合性较强,是中考常见题,熟练掌握平面图形的基本性质是解题关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
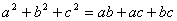 ,则△ABC是 三角形。
,则△ABC是 三角形。
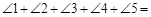 .
.