��Ŀ����
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���A��a��0����B��b��0��Ϊx�������㣬��C��Y����������ϣ���a��b�����ʽa2+2ab+b2=0��
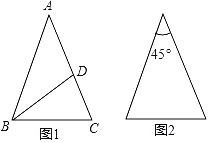
��1���жϡ�ABC����״��˵�����ɣ�
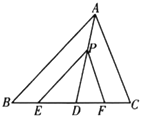
��2����ͼ2��M��N��OC�ϵĵ㣬�ҡ�CAM=��MAN=��NAB���ӳ�BN��AC��P������PM���ж�PM��AN��λ�ù�ϵ����֤����Ľ��ۣ�
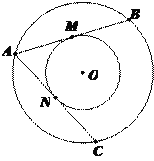
��3����ͼ3������DΪ�߶�BC�ϵĶ��㣨����B��C�غϣ�������D��DE��AB��E����GΪ�߶�DE��һ�㣬�ҡ�BGE=��ACB��FΪAD���е㣬����CF��FG����֤��CF��FG��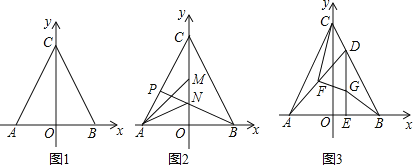
���𰸡���1����ABC�ǵ��������Σ���2��PM��AN��֤������������3��������
��������
��1��������ɵ�a=-b����OA=OB�������߶δ�ֱƽ���ߵ����ʿɵ�AC=BC������ABC�ǵ��������Σ�
��2���ӳ�AN��BC�ڵ�E������PM������M��MH��AE��MD��BP��MG��AC�����ݵ��������ε����ʿɵá�NAB=��NBA����ANO=��BNO���ɵá�PNC=��CNE�����ݽ�ƽ���ߵ����ʿɵ�PMƽ�֡�CPB�����������ε���ǵ����ʿɵá�CPM=��CAN=2��NAB�����ɵ�PM��AN��
��3���ӳ�GF����M��ʹFM=FG������CG��CM��AM���������֤��AMF�ա�DGF���ɵ�AM=DG���ɽǵ�������ϵ�ɵá�BCO=��BDG=��DBG����DG=BG�����ݡ�SAS����֤��AMC�ա�BGC���ɵ�CM=CG�����ݵ������������ʿɵ�CF��FG��
�⣺��1����a2+2ab+b2=0��
�ࣨa+b��2=0��
��a=-b��
��OA=OB����AB��OC��
��OC��AB�Ĵ�ֱƽ���ߣ�
��AC=BC��
���ACB�ǵ���������