��Ŀ����
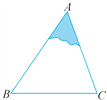
����Ŀ����ƽ��ֱ������ϵ�У���C������Ϊ��0��1.5�������ǰ��Ե�CΪԲ�ģ��뾶Ϊ1.5��Բ��Ϊ��C������Ȧ��Բ���ϵ�ÿһ���������C��һ�����ѣ�
��1��д����C�������������ꣻ
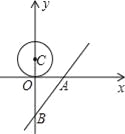
��2��ֱ��l�Ľ���ʽ��y=![]() x��4����x�ᡢy��ֱ���A��B���㣬Բ��C�ӵ㣨0��1.5����ʼ��ÿ��0.5����λ���ٶ�����y�������˶�������C������Ȧ�к�������ֱ����ʱ��ֱ�߽�����Ӱ�죬���ڵ�C�����˶��Ĺ����У�ֱ������Ӱ���ʱ�䣻
x��4����x�ᡢy��ֱ���A��B���㣬Բ��C�ӵ㣨0��1.5����ʼ��ÿ��0.5����λ���ٶ�����y�������˶�������C������Ȧ�к�������ֱ����ʱ��ֱ�߽�����Ӱ�죬���ڵ�C�����˶��Ĺ����У�ֱ������Ӱ���ʱ�䣻
��3��������y=ax2+bx+c��ԭ��O�͵�A���Ҷ���Dǡ��Ϊ��C�ĺ��ѣ�����OD��EΪ��C��һ�㣬����DOE������ʱ�����E�����꣬��ʱ��DOE������Ƕ��٣�
���𰸡���1���㣨0��0������0��3��Ϊ��C�ĺ��ѣ���2���ڵ�C�����˶��Ĺ����У�ֱ������Ӱ���ʱ��Ϊ6��t��16����3������DOE������ʱ����E������Ϊ����![]() ��
�� ![]() ������ʱ��DOE�������
������ʱ��DOE�������![]() ��
��
�������������������1��������Ȧ�Լ����ѵĶ��壬���ͼ�Σ����ɵó����ۣ���2����Բ��C�����˶���t�룬���C������Ϊ��0��1.5��0.5t�������ݺ��ѵĶ��壬��ϵ�C��ֱ��l�ľ���С�ڵ���1.5�����ɵó�����ʱ��t�ĺ�����ֵ���ŵ�һԪһ�η��̣��ⷽ�̼��ɵó����ۣ���3�����ݶ��κ����������ҳ������ߵĶԳ��ᣬ��Ϻ���ͼ���Լ����ѵĶ����ҳ���D�����ꣻ����OD������C��CM��OD�ڵ�M���ӳ�MC��ԲC�ڵ�E������EO��ED��ͨ��������������ֱ������������߶�EM�ij����ٽ�������ε������ʽ�������S��DOE��ֵ���ɵ�C��M����������ô���ϵ�������ֱ��CM�Ľ���ʽ�������E�����꣬�ٽ�������ľ��빫ʽ���������E�����꣬����ý⣮
�����������1��1.5��1.5=0��1.5+1.5=3��
���㣨0��0������0��3������C�ľ���Ϊ1.5��
���㣨0��0������0��3��Ϊ��C�ĺ��ѣ�
��2����Բ��C�����˶���t�룬���C������Ϊ��0��1.5��0.5t����
ֱ��l��y=![]() x��4�ɱ���Ϊ4x��3y��12=0��
x��4�ɱ���Ϊ4x��3y��12=0��
��C��ֱ��l�ľ���d=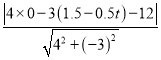 =|0.3t��3.3|��
=|0.3t��3.3|��
��ֱ����ԲCӰ��ʱ����d��1.5����|0.3t��3.3|��1.5��
��ã�6��t��16��
���ڵ�C�����˶��Ĺ����У�ֱ������Ӱ���ʱ��Ϊ6��t��16��
��3����y=![]() x��4��y=0����
x��4��y=0����![]() x��4=0��
x��4=0��
��ã�x=3������A������Ϊ��3��0����
�������⻭��ͼ�Σ���ͼ1��ʾ��
��������y=ax2+bx+c��ԭ��O�͵�A����O��0��0������A��3��0����
�������ߵĶԳ���Ϊx=![]() =1.5��
=1.5��
����Dǡ��Ϊ��C�ĺ��ѣ�
����D��������1.5��1.5����
����OD������C��CM��OD�ڵ�M���ӳ�MC��ԲC�ڵ�E������EO��ED����ʱS��DOE�����ͼ2��ʾ��
��OD��ԲC���ң�CM��OD��
����MΪ�߶�OD���е㣬
����M��������![]() ��
�� ![]() ����OM=
����OM=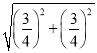 =
=![]() ��
��
��Rt��CMO��OM=![]() ��CO=1.5=
��CO=1.5=![]() ��
��
��CM=![]() =
=![]() ��
��
��CE=1.5=![]() ��EM=EC+CM��
��EM=EC+CM��
��EM=![]() ��
��
��ʱS��DOE=![]() ODEM=OMEM=
ODEM=OMEM=![]() ��
��![]() =
=![]() ��
��
��ֱ��CM�Ľ���ʽΪy=mx+n��
����C��������0��1.5������M��������![]() ��
�� ![]() ������0.75��0.75����
������0.75��0.75����
��![]() ����ã�
����ã� ![]() ��
��
��ֱ��CM�Ľ���ʽΪy=��x+1.5��
���E��������x����x+1.5����x��0����
��EC=![]() =1.5��
=1.5��
��x=��![]() ����x=
����x=![]() ����ȥ����
����ȥ����
����E����������![]() ��
�� ![]() ����
����
�ʵ���DOE������ʱ����E������Ϊ����![]() ��
�� ![]() ������ʱ��DOE�������
������ʱ��DOE�������![]() ��
��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�