Question

已知等腰三角形ABC中，AB=AC，AD平分∠BAC交于BC于 D点，在AD上任取一点P，（A点除外），过P点作EF∥AB，分别交AC、BC于点E、F，作PM∥AC，交AB于点M，连结ME。

（1）求证：四边形AEPM为菱形；

（2）当P点在何处时，菱形AEPM的面积为四边形EFBM面积的一半。

 

 

 

Answer 1

（1）见解析（2）P为EF中点时

解析:（1）证明：∵EF∥AB. PM∥AC。

∴AEPM为平行四边形。

∵AB=AC.AD平分∠CAB.

∴∠CAD=∠BAD.AD⊥BC.

           又∵∠BAD=∠EPA.

            ∴∠CAD=∠EPA.∴EA=EP.

            ∴AEPM为菱形。

       （2）解：当P为EF中点时。S_菱形AEPM=S_{四边形EFBM.}

              ∵四边形AEPM为菱形。

              ∴AD⊥EM.

             又∵AD⊥BC.

                ∴EM∥BC

             又∵EF∥AB.

               ∴四边形EFBM为平行四边形。

             作EN⊥AB于点N。

               ∴S_菱形AEPM=EP×EN=EF×EN=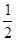S  _EMBF.

（1）先证明AEPM为平行四边形，再证得EA=EP最后得出结论

（2）设P为EF中点，进行求证