Question

已知⊙O₁的半径为3

5

cm，⊙O₂的半径为5cm，与⊙O₁相交于点D、E．若两圆的公共弦DE的长是6cm（圆心O₁、O₂在公共弦DE的两侧），则两圆的圆心距O₁O₂的长为（　　）

• A、2cm
• B、10cm
• C、2cm或10cm
• D、4cm

Answer 1

分析：根据相交两圆的性质知，连心线垂直平分公共弦可构造两个直角三角形，利用勾股定理即可求O₁M=4，O₂M=6，相加即可求解．

解答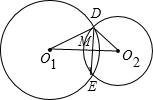：解：根据题意作图如下：
∵DE=6cm，O₁D=5cm，O₂D=3

5

cm，O₁O₂垂直平分DE，
∴DM=3cm，
∴O₁M=6cm，O₂M=4cm，
∴O₁O₂=10cm或O₁O₂=2cm，
∵若圆心O₁、O₂在公共弦DE的两侧，
∴O₁O₂=10cm．
故选B．

点评：主要考查了相交两圆的性质中，连心线垂直平分公共弦．要会利用该性质构造直角三角形，使用直角三角形中的勾股定理解题．