题目内容
如图,在梯形ABCD中,AD∥BC,M、N分别是两条对角线BD、AC的中点,
说明:MN∥BC且MN=
(BC-AD).
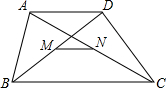
说明:MN∥BC且MN=
| 1 |
| 2 |

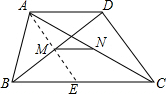
证明:连接AM并延长交BC于点E,
∵四边形ABCD是梯形,AD∥BC,
∴∠MAD=∠MEB,∠MDA=∠MBE,
又M为BD的中点,
∴MD=MB,
∴△AMD≌△EMB,
∴AD=BE,AM=ME.
∴M为AE中点,
∵N为AC中点,
∴MN为△AEC的边EC的中位线,
∴MN∥BC,且MN=
EC=
(BC-BE)=
(BC-AD).
∵四边形ABCD是梯形,AD∥BC,
∴∠MAD=∠MEB,∠MDA=∠MBE,
又M为BD的中点,
∴MD=MB,
∴△AMD≌△EMB,
∴AD=BE,AM=ME.
∴M为AE中点,
∵N为AC中点,
∴MN为△AEC的边EC的中位线,
∴MN∥BC,且MN=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目




