题目内容
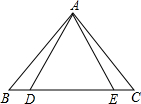
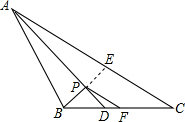
如图,△ABC中,AD为∠BAC的平分线,点F是BC的中点,BP⊥AD于D,AC=12,AB=8,求PF的长.


延长BP交AC于点E,
∵AD为∠BAC的平分线,
∴∠BAP=∠EAP,
∵BP⊥AD于D,
∴∠APB=∠APE=90°,
在△APB和△APE中,
∵
,
∴△APB≌△APE(ASA),
∴AB=AE=8,
∵AC=12,
∴EC=12-8=4,
∵△APB≌△APE,
∴BP=EP,
∵F是BC的中点,
∴PF=
EC=
×4=2.
∵AD为∠BAC的平分线,
∴∠BAP=∠EAP,
∵BP⊥AD于D,
∴∠APB=∠APE=90°,
在△APB和△APE中,
∵
|
∴△APB≌△APE(ASA),
∴AB=AE=8,
∵AC=12,
∴EC=12-8=4,
∵△APB≌△APE,
∴BP=EP,
∵F是BC的中点,
∴PF=
| 1 |
| 2 |
| 1 |
| 2 |


练习册系列答案
相关题目