题目内容
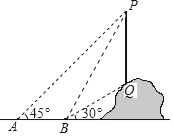
【题目】如图1,点![]() 为正
为正![]() 的
的![]() 边上一点(
边上一点(![]() 不与点
不与点![]() 重合),点
重合),点![]() 分别在边
分别在边![]() 上,且
上,且![]() .
.
(1)求证:![]() ;
;
(2)设![]() ,
,![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() (用含
(用含![]() 的式子表示);
的式子表示);
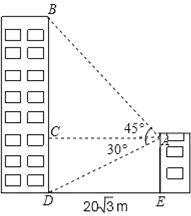
(3)如图2,若点![]() 为
为![]() 边的中点,求证:
边的中点,求证: ![]() .
.
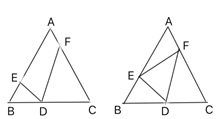
图1 图2
【答案】(1)详见解析;(2)详见解析;(3)详见解析.
【解析】
(1)根据两角对应相等的两个三角形相似即可判断;
(2)如图2中,分别过E,F作EG⊥BC于G,FH⊥BC于H,S1=![]() BDEG=
BDEG=![]() BDEG=
BDEG=![]() aBEsin60°=
aBEsin60°=![]() aBE,S2=
aBE,S2=![]() CDFH=
CDFH=![]() bCF,可得S1S2=
bCF,可得S1S2=![]() abBECF,由(1)得△BDE∽△CFD,
abBECF,由(1)得△BDE∽△CFD,![]() ,即BEFC=BDCD=ab,即可推出S1S2=
,即BEFC=BDCD=ab,即可推出S1S2=![]() a2b2;
a2b2;
(3)想办法证明△DFE∽△CFD,推出![]() ,即DF2=EFFC;
,即DF2=EFFC;
(1)证明:如图1中,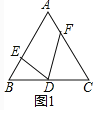
在△BDE中,∠BDE+∠DEB+∠B=180°,又∠BDE+∠EDF+∠FDC=180°,
∴∠BDE+∠DEB+∠B=∠BDE+∠EDF+∠FDC,
∵∠EDF=∠B,
∴∠DEB=∠FDC,
又∠B=∠C,
∴△BDE∽△CFD.
(2)如图2中,分别过E,F作EG⊥BC于G,FH⊥BC于H,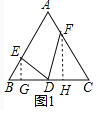
S1=![]() BDEG=
BDEG=![]() BDEG=
BDEG=![]() aBEsin60°=
aBEsin60°=![]() aBE,S2=
aBE,S2=![]() CDFH=
CDFH=![]() bCF,
bCF,
∴S1S2=![]() abBECF
abBECF
由(1)得△BDE∽△CFD,
∴![]() ,即BEFC=BDCD=ab,
,即BEFC=BDCD=ab,
∴S1S2=![]() a2b2.
a2b2.
(3)由(1)得△BDE∽△CFD,
∴![]() ,
,
又BD=CD,
∴![]() ,
,
又∠EDF=∠C=60°,
∴△DFE∽△CFD,
∴![]() ,即DF2=EFFC.
,即DF2=EFFC.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目