题目内容
二次函数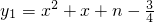 的图象与x轴只有一个交点;另一个二次函数
的图象与x轴只有一个交点;另一个二次函数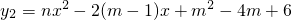 的图象与x轴交于两点,这两个交点的横坐标都是整数,且m是小于5的整数.
的图象与x轴交于两点,这两个交点的横坐标都是整数,且m是小于5的整数.
求:(1)n的值;
(2)二次函数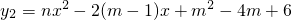 的图象与x轴交点的坐标.
的图象与x轴交点的坐标.
解:(1)∵二次函数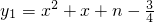 的图象与x轴只有一个交点,
的图象与x轴只有一个交点,
∴b2-4ac=1-4(n- )=0,
)=0,
解得:n=1;
(2)将n=1代入二次函数解析式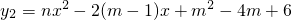 得:
得:
y2=x2-2(m-1)x+m2-4m+6,
∵二次函数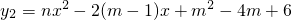 的图象与x轴交于两点,
的图象与x轴交于两点,
∴b2-4ac=[-2(m-1)]2-4(m2-4m+6)>0,
解得:m> ,
,
∵m是小于5的整数,
∴ <m<5,
<m<5,
∴m=3或4,
∵二次函数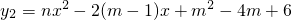 的图象与x轴交点的横坐标都是整数,
的图象与x轴交点的横坐标都是整数,
∴当m=3时,
y2=x2-4x+3=(x-1)(x-3),
与x轴交点坐标为;(1,0),(3,0),
当m=4时,
y2=x2-6x+6=(x-1)(x-3),
与x轴交点坐标为;(3+ ,0),(3-
,0),(3- ,0)不合题意舍去,
,0)不合题意舍去,
故二次函数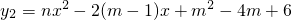 的图象与x轴交点的坐标为:(1,0),(3,0).
的图象与x轴交点的坐标为:(1,0),(3,0).
分析:(1)利用抛物线图象与x轴交点个数与△符号的关系得出b2-4ac=0求出即可;
(2)根据(1)中所求以及b2-4ac=[-2(m-1)]2-4(m2-4m+6)>0,得出m的取值范围,进而利用图象与x轴交点的横坐标都是整数得出m的值,进而得出答案.
点评:此题主要考查了抛物线与x轴交点问题与判别式△的关系和一元二次方程的解法等知识,熟练掌握△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点是解题关键.
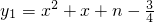 的图象与x轴只有一个交点,
的图象与x轴只有一个交点,∴b2-4ac=1-4(n-
 )=0,
)=0,解得:n=1;
(2)将n=1代入二次函数解析式
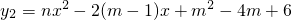 得:
得:y2=x2-2(m-1)x+m2-4m+6,
∵二次函数
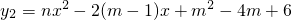 的图象与x轴交于两点,
的图象与x轴交于两点,∴b2-4ac=[-2(m-1)]2-4(m2-4m+6)>0,
解得:m>
 ,
,∵m是小于5的整数,
∴
 <m<5,
<m<5,∴m=3或4,
∵二次函数
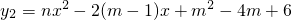 的图象与x轴交点的横坐标都是整数,
的图象与x轴交点的横坐标都是整数,∴当m=3时,
y2=x2-4x+3=(x-1)(x-3),
与x轴交点坐标为;(1,0),(3,0),
当m=4时,
y2=x2-6x+6=(x-1)(x-3),
与x轴交点坐标为;(3+
 ,0),(3-
,0),(3- ,0)不合题意舍去,
,0)不合题意舍去,故二次函数
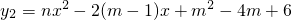 的图象与x轴交点的坐标为:(1,0),(3,0).
的图象与x轴交点的坐标为:(1,0),(3,0).分析:(1)利用抛物线图象与x轴交点个数与△符号的关系得出b2-4ac=0求出即可;
(2)根据(1)中所求以及b2-4ac=[-2(m-1)]2-4(m2-4m+6)>0,得出m的取值范围,进而利用图象与x轴交点的横坐标都是整数得出m的值,进而得出答案.
点评:此题主要考查了抛物线与x轴交点问题与判别式△的关系和一元二次方程的解法等知识,熟练掌握△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点是解题关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
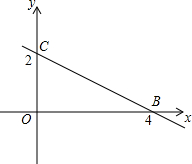 为y=ax2-3ax-4a(a<0).
为y=ax2-3ax-4a(a<0).