题目内容
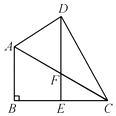
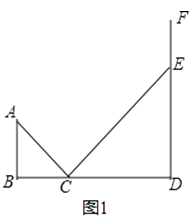
【题目】已知:如图,∠B=90°,AB∥DF,AB=4cm,BD=10cm,点C是线段BD上一动点,点E是直线DF上一动点,且始终保持AC⊥CE. 
(1)如图1试说明:∠ACB=∠CED.
(2)若AC=CE,试求DE的长.
【答案】
(1)解:如图1,∵AB∥DF,∠B=90°,
∴∠EDC=180°﹣∠ABC=90°,
∴∠CED+∠ECD=90°,
∵AC⊥CE,
∴∠ACE=90°,
∴∠ACB+∠ECD=90°,
∴∠ACB=∠CED
(2)解:如图2,∵∠EDC=90°,∠B=90°,
∴∠B=∠EDC,
由(1)可得,∠ACB=∠CED,
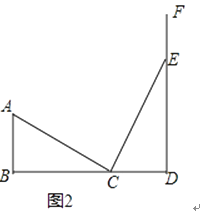
在△ABC和△CDE中,
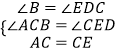 ,
,
∴△ABC≌△CDE,
∴DE=BC,AB=CD=4(cm),
∴BC=BD﹣CD=10﹣4=6(cm),
∴DE=6(cm)
【解析】(1)根据∠EDC=90°,得出∠CED+∠ECD=90°,再根据∠ACE=90°,得出∠ACB+∠ECD=90°,最后根据同角的余角相等,即可得出∠ACB=∠CED;(2)先判定△ABC≌△CDE,得出DE=BC,AB=CD=4(cm),进而得出BC=BD﹣CD=10﹣4=6(cm),根据全等三角形的对应边相等,即可得出DE=6(cm).

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
【题目】某市民政部门举行“即开式福利彩票”销售活动,发行彩票10万张(每张彩票2元),在这些彩票中,设置如下奖项:
奖金(元) | 10000 | 5000 | 1000 | 500 | 100 | 50 |
数量(个) | 1 | 4 | 20 | 40 | 100 | 200 |
如果花2元购买1张彩票,那么所得奖金不少于1000元的概率是