题目内容
【题目】如图,已知△ABC为等边三角形,D为BC延长线上的一点,CE平分∠ACD, CE=BD,求证: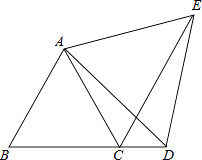
(1)△ABD≌△ACE;
(2)△ADE为等边三角形.
【答案】
(1)证明:∵△ABC等边三角形,
∴AB=AC,∠BAC=∠B=∠ACB=60°,
∴∠ACD=120°,
∵CE平分∠ACD,
∴∠ACE= ![]() ∠ACD=60°,
∠ACD=60°,
∴∠ACE=∠B,
在△ABD和△ACE中
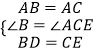
∴△ABD≌△ACE(SAS)
(2)证明:∵△ABD≌△ACE,
∴AD=AE,∠CAE=∠BAD,
∴∠DAE=∠BAC=60°,
∴△ADE为等边三角形
【解析】(1)根据等边三角形的性质得出AB=AC,∠BAC=∠B=∠ACB=60°,求出∠ACE=∠B,根据SAS推出全等即可;(2)根据全等三角形的性质得出AD=AE,∠CAE=∠BAD,求出∠DAE=∠BAC=60°,根据等边三角形的性质得出即可.

练习册系列答案
相关题目