��Ŀ����
����Ŀ����ͼ1��ֱ��l1��y=��![]() x+3��������ֱ��ڵ�A��B����ֱ��l2��y=x���ڵ�C��
x+3��������ֱ��ڵ�A��B����ֱ��l2��y=x���ڵ�C��
��1����A��B��������ꣻ
��2������BOC�������
��3����ͼ2������һ����ֱ��x���ֱ��l��ÿ��1����λ���ٶȴӵ�A����������AO���������ٻ������ֱ�ֱ��l1��l2��x���ڵ�M��N��Q�����˶�ʱ��Ϊt��s��������CQ��
����OA=3MNʱ����t��ֵ��
����̽��������ƽ�����Ƿ���ڵ�P��ʹ����O��Q��C��PΪ������ı��ι������Σ������ڣ���ֱ��д��t��ֵ���������ڣ���˵�����ɣ�



���𰸡���1��A��6��0��B��0��3������2��S��OBC=3����3����t=![]() ��
��![]() ����t=��6+2
����t=��6+2![]() ��s��6��2
��s��6��2![]() ��s��2s��4sʱ����O��Q��C��PΪ������ı��ι������Σ�
��s��2s��4sʱ����O��Q��C��PΪ������ı��ι������Σ�
��������
��1�����ô���ϵ�������ɽ�����⣻
��2������������ȷ����C���꼴�ɽ�����⣻
��3�����ݾ���ֵ���̼��ɽ�����⣻
��4���������������ۣ���OCΪ���εı�ʱ���ɵ�Q1![]() Q2
Q2![]() Q4��4��0������OCΪ���εĶԽ���ʱ��Q3��2��0����
Q4��4��0������OCΪ���εĶԽ���ʱ��Q3��2��0����
��1������ֱ��![]() ����x=0�õ�y=3����y=0���õ�x=6��
����x=0�õ�y=3����y=0���õ�x=6��
A��6��0��B��0��3����
��2���� ���
���![]() ��
��
��C��2��2����
��![]()
��3���١�![]()
��![]()
��OA=3MN��
��![]()
���t=![]() ��
��![]()
����ͼ3�У�������![]()
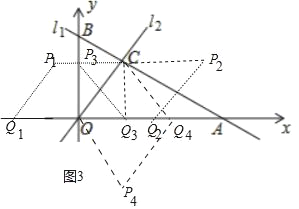
��OCΪ���εı�ʱ���ɵ�Q1����2![]() ��0����Q2��2
��0����Q2��2![]() ��0����Q4��4��0����
��0����Q4��4��0����
��OCΪ���εĶԽ���ʱ��Q3��2��0����
��t=��6+2![]() ��s��6��2
��s��6��2![]() ��s��2s��4sʱ����O��Q��C��PΪ������ı��ι������Σ�
��s��2s��4sʱ����O��Q��C��PΪ������ı��ι������Σ�

����Ŀ��ij�о���֪ʶ������AУ��BУ���ɳ�5��ѡ����ɴ����ӲμӾ�������У�ɳ�ѡ�ֵľ����ɼ���ͼ��ʾ��
(1)����ͼʾ��д�±���
ƽ����/�� | ��λ��/�� | ����/�� | |
AУ | ______ | 85 | ______ |
BУ | 85 | ______ | 100 |
(2)�����У�ɼ���ƽ��������λ���������ĸ�ѧУ�ľ����ɼ��Ϻã�
(3)������У�����ɼ��ķ�����ж��ĸ�ѧУ������ѡ�ֳɼ���Ϊ�ȶ���





