题目内容
如图，∠1=∠2，AC=6，AB=12，AE=4，AF=8．试说明：∠ACE=∠ABF．
解：∵AC=6，AB=12，AE=4，AF=8，
∴
=
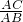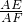=2，
∵∠1=∠2，
∴△ACE∽△ABF，
∴∠ACE=∠ABF．
分析：先根据已知条件判断出△ACE∽△ABF，再根据相似三角形的对应角相等即可解答．
点评：本题比较简单，考查的是相似三角形的判定定理及性质，根据题中所给的数据判断出两三角形的对应边成比例是解答此题的关键．
∴
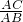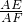==2，∵∠1=∠2，
∴△ACE∽△ABF，
∴∠ACE=∠ABF．
分析：先根据已知条件判断出△ACE∽△ABF，再根据相似三角形的对应角相等即可解答．
点评：本题比较简单，考查的是相似三角形的判定定理及性质，根据题中所给的数据判断出两三角形的对应边成比例是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
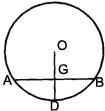14、如图，已知⊙P的半径OD=5，OD⊥AB，垂足是G，OG=3，则弦AB=
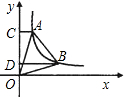如图，已知A，B两点是反比例函数y=
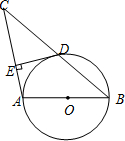如图AB是⊙O的直径，⊙O过BC的中点D，且DE⊥AC于点E．