题目内容
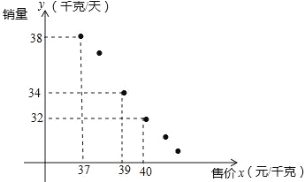
【题目】某进口专营店销售一种“特产”,其成本价是20元/千克,根据以往的销售情况描出销量y(千克/天)与售价x(元/千克)的关系,如图所示.
(1)试求出y与x之间的一个函数关系式;
(2)利用(1)的结论:
①求每千克售价为多少元时,每天可以获得最大的销售利润.
②进口产品检验、运输等过程需耗时5天,该“特产”最长的保存期为一个月(30天),若售价不低于30元/千克,则一次进货最多只能多少千克?
【答案】(1)函数关系式为y=﹣2x+112;(2)①每千克售价为38元时,每天可以获得最大的销售利润;②一次进货最多只能是1300千克.
【解析】
试题分析:(1)根据图中的信息可看出,图形经过(37,38),(39,34),(40,32),根据待定系数法可求函数关系式;(2)①根据函数的最值问题即可求解;②根据“特产”的保存时间和运输路线的影响,“特产”的销售时间最多是25天.要想使售价不低于30元/千克,就必须在最多25天内卖完,当售价为30元/千克时,销售量已经由(1)求出,因此可以根据最多进货的量÷30元/千克时的销售量≤25天,由此来列不等式,求出最多的进货量.
试题解析:(1)设y与x之间的一个函数关系式为y=kx+b,则![]() ,
,
解得![]() .
.
故函数关系式为y=﹣2x+112;
(2)①依题意有
w=(x﹣20)(﹣2x+112)=﹣2(x﹣38)2+324,
故每千克售价为38元时,每天可以获得最大的销售利润;
②由题意可得,售价越低,销量越大,即能最多的进货,
设一次进货最多m千克,
则![]() ≤30﹣5,
≤30﹣5,
解得:m≤1300.
故一次进货最多只能是1300千克.

练习册系列答案
相关题目