Question

【题目】如图1，矩形ABCD中，AB＝，AD＝4，在BC边上取点E，使BE＝AB，将△ABE向左平移到△DCF的位置，得到四边形AEFD．

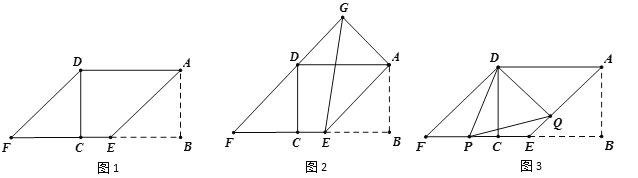
（1）求证：四边形AEFD是菱形；

（2）如图2，将△DCF绕点D旋转至△DGA，连接GE，求线段GE的长；

（3）如图3，设P、Q分别是EF、AE上的两点，且∠PDQ=67.5°，试探究线段PF、AQ、PQ之间的数量关系，并说明理由．

Answer 1

【答案】（1）见解析；（2）；（3）PQ2＝PF2+AQ2，理由见解析

【解析】

（1）根据平移的性质得到AE∥DF，AE＝DF，则由此判断四边形AEFD是平行四边形，然后由：邻边相等的平行四边形是菱形，证得结论；

（2）根据勾股定理，即可求解；（3）如下图，作辅助线，构建三角形全等，证明△PDQ≌△GDQ，得PQ＝GQ，在Rt△AGQ中，根据勾股定理可得结论．

（1）由平移，得AE∥DF，AE＝DF，

∴四边形AEFD是平行四边形．

∵矩形ABCD，∴∠B=90°，∵BE=AE＝，

∴AE＝4，

又∵AE＝AD＝4，

∴四边形AEFD是菱形．

（2）由（1）得：△ABE是等腰直角三角形∴∠AEB=45°，

∵AE∥DF，

∴∠F=∠AEB=45°，

∵矩形ABCD，∴AD∥BC

∴∠DAE=∠AEB=45°，

∴∠GAE=90°，

∵△DCF绕点D旋转得到△DGA，

∴GA=CF＝，

∴．

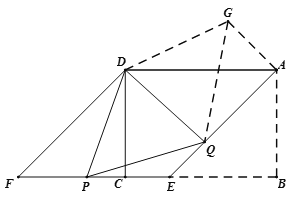
（3）PF、AQ、PQ之间的数量关系为：

PQ2＝PF2+AQ2．

理由如下：

由（2）得：∠AEB=45°，∴∠ADF=∠AEF=135°，∵AD＝DF，

∴将△DFP绕点D逆时针旋转135°得△DAG，

连GQ，如图，∴GA＝PF，DG＝DP，∠GDA＝∠PDF，∠GAD＝∠F=45°，

∴∠GAQ＝∠GAD+∠DAE＝90°，

∴GQ2＝GA2+AQ2＝PF2+AQ2；

又∵∠ADF＝135°，而∠PDQ＝67.5°，∴∠PDF+∠ADQ＝135°﹣67.5°＝67.5°，

∴∠GDA+∠ADQ＝∠GDQ=67.5°，∴∠PDQ＝∠GDQ

而DG＝DP，DQ为公共边，∴△PDQ≌△GDQ，

∴PQ＝GQ，

∴PQ2＝PF2+AQ2．