题目内容
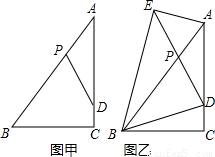
如图,在Rt△ABC中,∠ACB=Rt∠,BC=3,AC=4,D在AC上,CD=1,P是边AB上的一动点,设BP=m.(1)如图甲,当m为何值时,△ADP与△ABC相似;
(2)如图乙,延长DP至点E,使EP=DP,连结AE,BE.
①四边形AEBC的面积S会随m的变化而变化吗?若不变,求出S的值;若变化,求出S与m的函数关系式;
②作点E关于直线AB的对称点Eˊ,连结BD,当∠DBA=2∠DEEˊ时,求m的值.
【答案】分析:(1)根据若△ADP与△ABC相似,则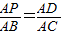 或
或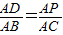 ,列出算式,再计算即可.
,列出算式,再计算即可.
(2)①四边形AEBC的面积S不变,分别过D、E作DG⊥AB,EH⊥AB,则∠DGP=∠EHP=90°,再根据∠GPD=∠HPE,DP=EP,得出△DGP≌△EHP,DG=EH,再根据sin∠BAC= ,求出EH=DG=
,求出EH=DG= ×3,最后根据S四边形AEBC=S△ABC+S△ABE代入计算即可;
×3,最后根据S四边形AEBC=S△ABC+S△ABE代入计算即可;
②当E'在D的上方时,则 P E'=PE=PD,∠D E'E=90°,再根据∠DPE'=2∠DEE'=∠ABD,∠PDE'=∠PE'D,得出∠PDE'=∠BPD=∠PE'D=∠BDP,BP=BD=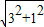 ,即可求出m,
,即可求出m,
当E'在D的下方时,记BD与PE'交于点F,先求出DE'=2PG=2(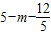 ),再根据BD=BF+DF=BP+DE'=m+
),再根据BD=BF+DF=BP+DE'=m+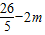 =
=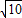 ,求出m即可.
,求出m即可.
解答: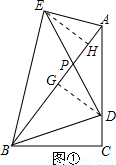 解:(1)若△ADP与△ABC相似,
解:(1)若△ADP与△ABC相似,
则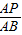 =
=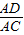 或
或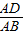 =
=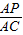 ,
,
 =
=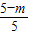 或
或 =
=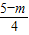 ,
,
∴m= 或m=
或m=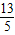 ,
,
综上所述,当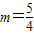 或
或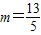 时,△ADP与△ABC相似;
时,△ADP与△ABC相似;
(2);①四边形AEBC的面积S不变,且S=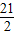 ,
,
理由如下:如图①:
分别过D、E作DG⊥AB,EH⊥AB,G、H为垂足,
∴∠DGP=∠EHP=90°,
又∵∠GPD=∠HPE,DP=EP,
∴△DGP≌△EHP,
∴DG=EH,
∵sin∠BAC=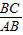 =
=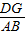 =
= ,
,
∴EH=DG= ×3=
×3= ,
,
∴S四边形AEBC=S△ABC+S△ABE= ×3×4+
×3×4+ ×5×
×5× =
=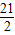 ;
;
②当E'在D的上方时,如图②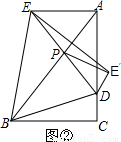
由题意,得 P E'=PE=PD,∠D E'E=90°,
∴∠DPE'=2∠DEE'=∠ABD,∠PDE'=∠PE'D
∴∠PDE'=∠BPD=∠PE'D=∠BDP
∴BP=BD=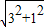 =
=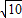
∴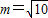 ;
;
当E'在D的下方时,如图③,记BD与PE'交于点F
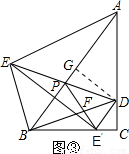 由(2)①,得 BF=BP,DF=DE',
由(2)①,得 BF=BP,DF=DE',
DE'=2PG=2(5-m-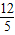 )=
)=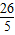 -2m,
-2m,
∴BD=BF+DF=BP+DE'
=m+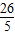 -2m,
-2m,
=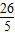 -m=
-m=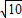 ,
,
∴m=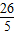
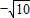 ;
;
综上所述,当m=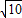 或m=
或m=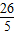
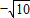 时,∠DBA=2∠DEE'.
时,∠DBA=2∠DEE'.
点评:此题考查了相似形综合,用到的知识点是相似三角形的判定与性质、勾股定理、锐角三角函数等,关键是根据题意画出图形,列出算式.
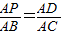 或
或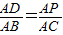 ,列出算式,再计算即可.
,列出算式,再计算即可.(2)①四边形AEBC的面积S不变,分别过D、E作DG⊥AB,EH⊥AB,则∠DGP=∠EHP=90°,再根据∠GPD=∠HPE,DP=EP,得出△DGP≌△EHP,DG=EH,再根据sin∠BAC=
 ,求出EH=DG=
,求出EH=DG= ×3,最后根据S四边形AEBC=S△ABC+S△ABE代入计算即可;
×3,最后根据S四边形AEBC=S△ABC+S△ABE代入计算即可;②当E'在D的上方时,则 P E'=PE=PD,∠D E'E=90°,再根据∠DPE'=2∠DEE'=∠ABD,∠PDE'=∠PE'D,得出∠PDE'=∠BPD=∠PE'D=∠BDP,BP=BD=
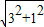 ,即可求出m,
,即可求出m,当E'在D的下方时,记BD与PE'交于点F,先求出DE'=2PG=2(
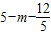 ),再根据BD=BF+DF=BP+DE'=m+
),再根据BD=BF+DF=BP+DE'=m+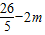 =
=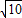 ,求出m即可.
,求出m即可.解答:
 解:(1)若△ADP与△ABC相似,
解:(1)若△ADP与△ABC相似,则
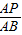 =
=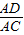 或
或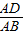 =
=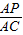 ,
, =
=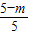 或
或 =
=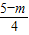 ,
,∴m=
 或m=
或m=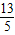 ,
,综上所述,当
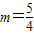 或
或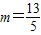 时,△ADP与△ABC相似;
时,△ADP与△ABC相似;(2);①四边形AEBC的面积S不变,且S=
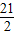 ,
,理由如下:如图①:
分别过D、E作DG⊥AB,EH⊥AB,G、H为垂足,
∴∠DGP=∠EHP=90°,
又∵∠GPD=∠HPE,DP=EP,
∴△DGP≌△EHP,
∴DG=EH,
∵sin∠BAC=
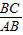 =
=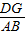 =
= ,
,∴EH=DG=
 ×3=
×3= ,
,∴S四边形AEBC=S△ABC+S△ABE=
 ×3×4+
×3×4+ ×5×
×5× =
=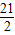 ;
;②当E'在D的上方时,如图②

由题意,得 P E'=PE=PD,∠D E'E=90°,
∴∠DPE'=2∠DEE'=∠ABD,∠PDE'=∠PE'D
∴∠PDE'=∠BPD=∠PE'D=∠BDP
∴BP=BD=
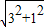 =
=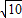
∴
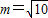 ;
;当E'在D的下方时,如图③,记BD与PE'交于点F
 由(2)①,得 BF=BP,DF=DE',
由(2)①,得 BF=BP,DF=DE',DE'=2PG=2(5-m-
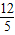 )=
)=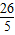 -2m,
-2m,∴BD=BF+DF=BP+DE'
=m+
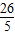 -2m,
-2m,=
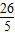 -m=
-m=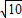 ,
,∴m=
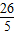
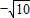 ;
;综上所述,当m=
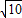 或m=
或m=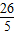
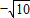 时,∠DBA=2∠DEE'.
时,∠DBA=2∠DEE'.点评:此题考查了相似形综合,用到的知识点是相似三角形的判定与性质、勾股定理、锐角三角函数等,关键是根据题意画出图形,列出算式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F.
(2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F. 如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,AD和BD分别是∠BAC和∠ABC的平分线,它们相交于点D,求点D到BC的距离.
如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,AD和BD分别是∠BAC和∠ABC的平分线,它们相交于点D,求点D到BC的距离. 边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直.
边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直. 如图,在Rt△ABC中,BD⊥AC,sinA=
如图,在Rt△ABC中,BD⊥AC,sinA= 点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).
点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).