题目内容
 如图,在直角坐标系中,已知P0的坐标为(1,0),将线段OP0绕O按逆时针方向旋转45°,再将其长度伸长为OP0的3倍,得到线段OP1;又将线段OP1绕O点按逆时针方向旋转45°,长度伸长为OP1的3倍,得到线段OP2;如此下去,得到线段OP3,OP4,…,Opn(n为正整数),则△P2009OP2010的面积________.
如图,在直角坐标系中,已知P0的坐标为(1,0),将线段OP0绕O按逆时针方向旋转45°,再将其长度伸长为OP0的3倍,得到线段OP1;又将线段OP1绕O点按逆时针方向旋转45°,长度伸长为OP1的3倍,得到线段OP2;如此下去,得到线段OP3,OP4,…,Opn(n为正整数),则△P2009OP2010的面积________.
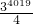

分析:求出OP1、OP2、OP3的长,得出规律求出OP2010的长,根据经过8次P8落在x轴的正半轴上,得到OP2010在y轴上,OP2009在第一象限角的平分线上,求出三角形的高,根据三角形的面积求出即可.
解答:
 解:OP1=3OP=3×1=3,
解:OP1=3OP=3×1=3,同理OP2=30P1=3×3×1=32,
OP3=3OP2=33,
…
OP2009=32009,OP2010=32010,
∵360°÷45°=8,
即经过8次P8落在x轴的正半轴上,
∴2010÷8=251…2,
即OP2010在y轴上,OP2009在第一象限角的平分线上,
如图:过P2009作P2009C⊥y轴于C,
由勾股定理求出P2009C=
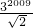 ,
,∴△OP2009P2010的面积是
 ×OP2010×CP2010=
×OP2010×CP2010= ×32010×
×32010×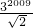 =
=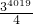
 ,
,故答案为:
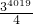
 .
.点评:本题考查了旋转的性质:旋转前后两图形全等,即对应线段相等,对应角相等.也考查了等腰三角形的性质.

练习册系列答案
相关题目

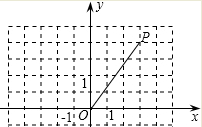 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
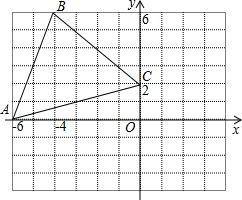 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: