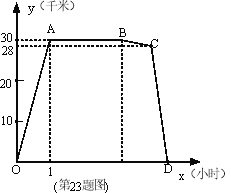
题目内容
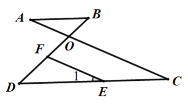
【题目】如图，AC与BD相交于点O，点E是CD上的一点，F是OD上的一点，且EF∥AC，∠1=∠A．
(1)求证：AB∥CD．
(2)若∠BFE=70°，求：∠AOB的度数．
【答案】（1）证明见解析，（2）
【解析】
（1）由EF∥AC，利用两直线平行同位角相等得到一对角相等，再由已知角相等，等量代换得到一对内错角相等，利用内错角相等两直线平行即可得证；
（2）由EF与AC平行，利用两直线平行同旁内角互补得到∠BFE+∠DOC=180°，结合对顶角相等即可求得结果．
（1）证明：∵EF∥AC，
∴∠1=∠C （ 两直线平行，同位角相等 ），
又∵∠1=∠A，
∴∠C=∠A，
∴AB∥CD，（内错角相等，两直线平行）
解：（2）∵FE∥AC，
∴∠BFE+∠DOC=180°（ 两直线平行，同旁内角互补 ），
又∵∠BFE=70°，
∴∠DOC=110°,
练习册系列答案
53随堂测系列答案
相关题目
