题目内容
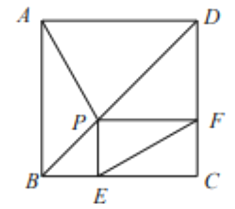
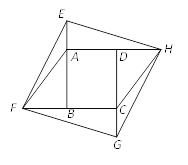
【题目】如图,将面积为![]() 的矩形ABCD的四边BA、CB、DC、AD分别延长至E、F、G、H,使得AE=CG,BF=BC, DH=AD,连接EF, FG,GH,HE,AF,CH.若四边形EFGH为菱形,
的矩形ABCD的四边BA、CB、DC、AD分别延长至E、F、G、H,使得AE=CG,BF=BC, DH=AD,连接EF, FG,GH,HE,AF,CH.若四边形EFGH为菱形,![]() ,则菱形EFGH的面积是( )
,则菱形EFGH的面积是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】B
【解析】
设FB=2a,AB=3a,由Rt△EBF≌Rt△GDH(HL),推出FB=DH,即得到BF=DH=AD=BC=2a,设AE=CG=x,由FG=GH,可得16a2+x2=(x+3a)2+4a2,解得x=![]() ,用a表示菱形的面积即可解决问题.
,用a表示菱形的面积即可解决问题.
解:∵FB:AB=2:3,
∴可以假设FB=2a,AB=3a,
∵四边形ABCD是矩形,
∴AD=BC,AB=CD,
∵AE=CG,
∴BE=GD,
∵∠EBF=∠GDH=90°,EF=GH,EB=GD,
∴Rt△EBF≌Rt△GDH(HL),
∴FB=DH,
∵AD=DH,
∴BF=DH=AD=BC=2a,设AE=CG=x,
∵FG=GH,
∴16a2+x2=(x+3a)2+4a2
解得x=![]()
∴S菱形EFGH=2×![]() ×2a×(3a+
×2a×(3a+![]() )+6a2+2×
)+6a2+2×![]() ×4a×
×4a×![]() =15a2
=15a2
∵S=6a2,
∴a2=![]()
∴菱形EFGH的面积=![]() S
S

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案【题目】某校的一个社会实践小组对本校学生中开展主题为“垃圾分类知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,划分等级后的数据整理如下表:
等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 |
频数 | 20 | 35 | 41 | 4 |
(1)请根据调查结果,若该校有学生![]() 人,请估计这些学生中“比较了解”垃圾分类知识的人数.
人,请估计这些学生中“比较了解”垃圾分类知识的人数.
(2)在“比较了解”的调查结果里,其中九(1)班学生共有![]() 人,其中
人,其中![]() 名男生和
名男生和![]() 名女生,在这
名女生,在这![]() 人中,打算随机选出
人中,打算随机选出![]() 位进行采访,求出所选两位同学恰好是1名男生和1名女生的概率.(要求列表或画树状图)
位进行采访,求出所选两位同学恰好是1名男生和1名女生的概率.(要求列表或画树状图)
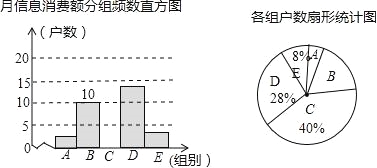
【题目】在信息快速发展的社会,“信息消费”已成为人们生活的重要组成部分.某高校组织课外小组在郑州市的一个社区随机抽取部分家庭,调查每月用于信息消费的金额,根据数据整理成如图所示的不完整统计表和统计图.已知A,B两组户数频数直方图的高度比为1:5.
月信息消费额分组统计表
组别 | 消费额(元) |
A | 10≤x<100 |
B | 100≤x<200 |
C | 20≤x<300 |
D | 300≤x<400 |
E | x≥400 |
请结合图表中相关数据解答下列问题:
(1)这次接受调查的有 户;
(2)在扇形统计图中,“E”所对应的圆心角的度数是 ;
(3)请你补全频数直方图;
(4)若该社区有2000户住户,请估计月信息消费额不少于200元的户数是多少?