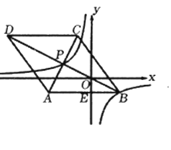
题目内容
【题目】如图,分别以△ABC的边AC和BC为腰向外作等腰直角△DAC和等腰直角△EBC,连接DE.

(1)求证:△DAC∽△EBC;
(2)求△ABC与△DEC的面积比.
【答案】(1)见解析;(2)![]()
【解析】
(1)利用等腰直角三角形的性质证明△DAC∽△EBC;
(2)依据△DAC∽△EBC所得条件,证明△ABC与△DEC相似,通过面积比等于相似比的平方得到结果.
(1)证明:∵△EBC是等腰直角三角形
∴BC=BE,∠EBC=90°
∴∠BEC=∠BCE=45°.
同理∠DAC=90°,∠ADC=∠ACD=45°
∴∠EBC=∠DAC=90°,∠BCE=∠ACD=45°.
∴△DAC∽△EBC.
(2)解:∵在Rt△ACD中, AC2+AD2=CD2,
∴2AC2=CD2
∴![]() ,
,
∵△DAC∽△EBC
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵∠BCE=∠ACD
∴∠BCE-∠ACE=∠ACD-∠ACE,即∠BCA=∠ECD,
∵在△DEC和△ABC中,![]() =
=![]() ,∠BCA=∠ECD,
,∠BCA=∠ECD,
∴△DEC∽△ABC,
∴S△ABC:S△DEC=![]() =
=![]() .
.

练习册系列答案
相关题目