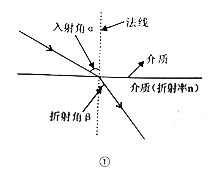
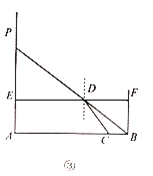
题目内容
【题目】![]() 、
、![]() 是半径为
是半径为![]() 的
的![]() 上的两条弦,且
上的两条弦,且![]() ,
,![]() ,那么,
,那么,![]() 的弦心距__________,圆周角
的弦心距__________,圆周角![]() 所对的弧等于__________.
所对的弧等于__________.
【答案】![]()
![]() 或
或![]()
【解析】
(1)作OF⊥AC于F,连接OA,根据垂径定理求出AF,根据勾股定理计算即可得出结论;
(2)连接OA,过O作OE⊥AB于E,OF⊥AC于F,根据垂径定理求出AE、FA值,根据解直角三角形的知识求出∠OAB和∠OAC,然后分两种情况求出∠BAC,再根据弧长公式计算即可.
解:(1) 如图,
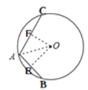
作OF⊥AC于F,连接OA,则AF= ![]() AC=
AC= ![]()
在Rt△OAF中,OF= ![]() =1,
=1,
故答案为1;
(2)有两种情况:
①如图所示:连接OA,过O作OE⊥AB于E,OF⊥AC于F,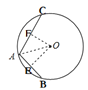
∴∠OEA=∠OFA=90°,
由垂径定理得:AE=BE= ![]() ,AF=CF=
,AF=CF=![]() ,
,
cos∠OAE=![]() =
=![]() ,cos∠OAF=
,cos∠OAF=![]() =
=![]() ,
,
∴∠OAE=45°,∠OAF=30°,
∴∠BAC=30°+45°=75°,
∴∠BOC=150°,
∴圆周角![]() 所对的弧长=
所对的弧长=![]() =
=![]() ;
;
②如图所示:
连接OA,过O作OE⊥AB于E,OF⊥AC于F,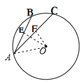
∴∠OEA=∠OFA=90°,
由垂径定理得:AE=BE= ![]() ,AF=CF=
,AF=CF=![]() ,
,
cos∠OAE=![]() =
=![]() ,cos∠OAF=
,cos∠OAF=![]() =
=![]() ,
,
∴∠OAE=45°,∠OAF=30°,
∴∠BAC=45°30°=15°,
∴∠BOC=30°,
∴圆周角![]() 所对的弧长=
所对的弧长=![]() =
=![]() ;
;
故答案为![]() 或
或![]() ,
,

【题目】为了解某校七年级学生的英语口语水平,随机抽取该年级部分学生进行英语口语测试,学生的测试成绩按标准定为A、B、C、D四个等级,并把测试成绩绘成如图所示的两个统计图表.
七年级英语口语测试成绩统计表
成绩 | 等级 | 人数 |
| A | 12 |
| B | m |
| C | n |
| D | 9 |
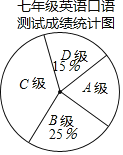
请根据所给信息,解答下列问题:
(1)本次被抽取参加英语口语测试的学生共有多少人?
(2)求扇形统计图中C级的圆心角度数;
(3)若该校七年级共有学生640人,根据抽样结课,估计英语口语达到B级以上![]() 包括B级
包括B级![]() 的学生人数.
的学生人数.
【题目】在“书香校园”活动中,某校为了解学生家庭藏书情况,随机抽取本校部分学生进行调查,并绘制成部分统计图表如下:
类别 | 家庭藏书m本 | 学生人数 |
A | 0≤m≤25 | 20 |
B | 26≤m≤50 | a |
C | 51≤m≤75 | 50 |
D | m≥76 | 66 |
根据以上信息,解答下列问题:
(1)该调查的样本容量为 ,a= ;
(2)随机抽取一位学生进行调查,刚好抽到A类学生的概率是 ;
(3)若该校有2000名学生,请估计全校学生中家庭藏书不少于76本的人数.
【题目】某篮球队对队员进行定点投篮测试,每人每天投篮10次,现对甲、乙两名队员在五天中进球数(单位:个)进行统计,结果如下:
甲 | 10 | 6 | 10 | 6 | 8 |
乙 | 7 | 9 | 7 | 8 | 9 |
经过计算,甲进球的平均数为8,方差为3.2.
(1)求乙进球的平均数和方差;
(2)如果综合考虑平均成绩和成绩稳定性两方面的因素,从甲、乙两名队员中选出一人去参加定点投篮比赛,应选谁?为什么?