题目内容
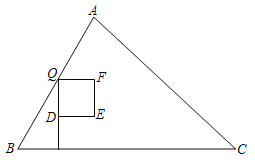
【题目】如图,顶点为M的抛物线y=ax2+bx+3与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.
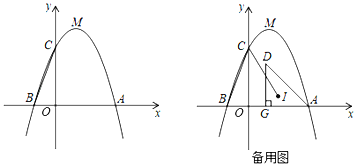
(1)求这条抛物线对应的函数表达式;
(2)问在y轴上是否存在一点P,使得△PAM为直角三角形?若存在,求出点P的坐标;若不存在,说明理由.
(3)若在第一象限的抛物线下方有一动点D,满足DA=OA,过D作DG⊥x轴于点G,设△ADG的内心为I,试求CI的最小值.
【答案】(1)y=﹣x2+2x+3;(2)存在,点P坐标为(0,﹣![]() )或(0,1)或(0,3)或(0,
)或(0,1)或(0,3)或(0,![]() ),理由见解析;(3)
),理由见解析;(3)![]()
【解析】
(1)将A(3,0),B(﹣1,0)两点的坐标代入y=ax2+bx+3即可求得答案;
(2)设点P坐标为(0,p),可求得顶点M(1,4),利用两点之间的距离公式分别求得![]() 、
、![]() 、
、![]() ,分类讨论计算:当∠PAM=90°、∠APM=90°、∠AMP=90°时p的值,从而得到结论;
,分类讨论计算:当∠PAM=90°、∠APM=90°、∠AMP=90°时p的值,从而得到结论;
(3)根据三角形内心的定义作三边的高线,根据三角形内心的性质知四边形IEGH是正方形,设点I坐标为(m,n),根据点的坐标的意义及切线长定理求得:AG=n+3﹣m,DG=m+n,由勾股定理DG2+AG2=DA2化简并配方得:(m﹣![]() )2+(n+
)2+(n+![]() )2=
)2=![]() ,逆用两点之间的距离公式知:点I(m,n)与定点Q(
,逆用两点之间的距离公式知:点I(m,n)与定点Q(![]() ,﹣
,﹣![]() )的距离为
)的距离为![]() ,当点I在线段CQ上时,CI最小,从而求得答案.
,当点I在线段CQ上时,CI最小,从而求得答案.
解:(1)∵抛物线y=ax2+bx+3过点A(3,0),B(﹣1,0)
∴![]() , 解得:
, 解得:![]() .
.
∴这条抛物线对应的函数表达式为y=﹣x2+2x+3.
(2)在y轴上存在点P,使得△PAM为直角三角形.
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴顶点M(1,4),
∴AM2=(3﹣1)2+42=20,
设点P坐标为(0,p),
①AP2=32+p2=9+p2,MP2=12+(4﹣p)2=17﹣8p+p2/span>
若∠PAM=90°,则AM2+AP2=MP2,
∴20+9+p2=17﹣8p+p2,解得:p=﹣![]() ,
,
∴P(0,﹣![]() );
);
②若∠APM=90°,则AP2+MP2=AM2,
∴9+p2+17﹣8p+p2=20,解得:p1=1,p2=3,
∴P(0,1)或(0,3);
③若∠AMP=90°,则AM2+MP2=AP2,
∴20+17﹣8p+p2=9+p2,解得:p=![]() ,
,
∴P(0,![]() )
)
综上所述,点P坐标为(0,﹣![]() )或(0,1)或(0,3)或(0,
)或(0,1)或(0,3)或(0,![]() )时,△PAM为
)时,△PAM为
直角三角形.
(3)如图,过点I作IE⊥x轴于点E,IF⊥AD于点F,IH⊥DG于点H
∵DG⊥x轴于点G,∴∠HGE=∠IEG=∠IHG=90°,∴四边形IEGH是矩形,
∵点I为△ADG的内心,∴IE=IF=IH,AE=AF,DF=DH,EG=HG,
∴矩形IEGH是正方形,
设点I坐标为(m,n),
∴OE=m,HG=GE=IE=n,
∴AF=AE=OA﹣OE=3﹣m,
∴AG=GE+AE=n+3﹣m,
∵DA=OA=3,
∴DH=DF=DA﹣AF=3﹣(3﹣m)=m,
∴DG=DH+HG=m+n,
∵DG2+AG2=DA2,∴(m+n)2+(n+3﹣m)2=32,
∴化简得:m2﹣3m+n2+3n=0,
配方得:(m﹣![]() )2+(n+
)2+(n+![]() )2=
)2=![]() ,
,
∴点I(m,n)与定点Q(![]() ,﹣
,﹣![]() )的距离为
)的距离为![]() ,
,
∴点I在以点Q(![]() ,﹣
,﹣![]() )为圆心,半径为
)为圆心,半径为![]() 的圆在第一象限的弧上运动,
的圆在第一象限的弧上运动,
∴当点I在线段CQ上时,CI最小,
∵CQ=![]() ,∴CI=CQ﹣IQ=
,∴CI=CQ﹣IQ=![]() ,
,
∴CI最小值为![]() .
.

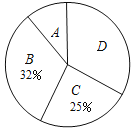
【题目】在“书香校园”活动中,某校为了解学生家庭藏书情况,随机抽取本校部分学生进行调查,并绘制成部分统计图表如下:
类别 | 家庭藏书m本 | 学生人数 |
A | 0≤m≤25 | 20 |
B | 26≤m≤50 | a |
C | 51≤m≤75 | 50 |
D | m≥76 | 66 |
根据以上信息,解答下列问题:
(1)该调查的样本容量为 ,a= ;
(2)随机抽取一位学生进行调查,刚好抽到A类学生的概率是 ;
(3)若该校有2000名学生,请估计全校学生中家庭藏书不少于76本的人数.