题目内容
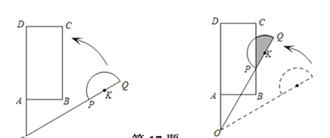
【题目】如图,点O是等边![]() 内一点
内一点![]() 将
将![]() 绕点C按顺时针方向旋转
绕点C按顺时针方向旋转![]() 得
得![]() ,连接
,连接![]() 已知
已知![]()
![]() .
.
![]() 求证:
求证:![]() 是等边三角形;
是等边三角形;
![]() 当
当![]() 时,试判断
时,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
![]() 探究:当
探究:当![]() 为多少度时,
为多少度时,![]() 是等腰三角形.
是等腰三角形.

【答案】(1)证明见解析(2)△AOD是直角三角形;(3)当α的度数为125°,或110°,或140°时,△AOD是等腰三角形
【解析】
本题是条件性开放题,要找到变化中的不变量才能有效解决问题,尤其是注意分类讨论.(1)由旋转性质,可知CD=CO,再加旋转角是60°, 根据有一个角是60°的等腰三角形是等边三角形即可解答;(2) 根据旋转性质得△BOC≌△ADC,所以∠ADC=∠BOC=150°,同(1)可知△COD是等边三角形,每个角等于60°,从而求得∠ADO=90°,即可解答;(3)需要进行分类讨论,分AO=AD,OA=OD,OD=AD三种情况,再根据等边对等角,![]() 是等边三角形;∠BOC=∠ADC=
是等边三角形;∠BOC=∠ADC=![]() ,即可解答.
,即可解答.

练习册系列答案
相关题目
【题目】某校共有1000名学生,为了了解他们的视力情况,随机抽查了部分学生的视力,并将调查的数据整理绘制成直方图和扇形图.

(1)这次共调查了多少名学生?扇形图中的![]() 、
、![]() 值分别是多少?
值分别是多少?
(2)补全频数分布直方图;
(3)在光线较暗的环境下学习的学生占对应被调查学生的比例如下表:
视力 |
| 0.35~0.65 | 0.65~0.95 | 0.95~1.25 | 1.25~l.55 |
比例 |
|
|
|
|
|
根据调查结果估计该校有多少学生在光线较暗的环境下学习?