题目内容
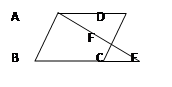
如图,在平行四边形ABCD中,E是BC延长线上一点,AE交CD于点F,且CE=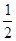 BC,则
BC,则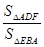 =
=
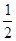 BC,则
BC,则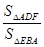 =
= 
A.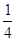 | B.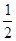 | C.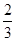 | D.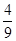 |
D
利用平行四边形的性质可以得到相似三角形,然后利用相似三角形的面积的比等于相似比可以得到答案.
解答:解:∵四边形ABCD是平行四边形,
∴AD∥BE,CD∥AB,
∴△ADF∽△ECF△ECF∽△EAB,
∴△ADF∽△EBA,
∵CE=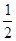 BC,
BC,
BE=CE+BC=CE+AD=3CE,
∴AD:BE=2:3,
∴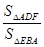 =
=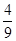 ,
,
故选D.
解答:解:∵四边形ABCD是平行四边形,
∴AD∥BE,CD∥AB,
∴△ADF∽△ECF△ECF∽△EAB,
∴△ADF∽△EBA,
∵CE=
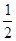 BC,
BC,BE=CE+BC=CE+AD=3CE,
∴AD:BE=2:3,
∴
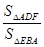 =
=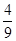 ,
,故选D.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
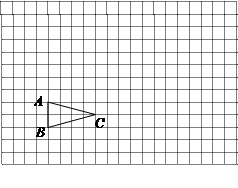
 点坐标;
点坐标;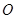 为旋转中心,将△ABC绕点
为旋转中心,将△ABC绕点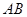 ,
,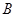 是
是 的中点,
的中点, 留在坡面上.已知铁塔底座宽
留在坡面上.已知铁塔底座宽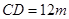 ,塔影长
,塔影长 ,小明和小华的身高都是1.5m, 同一时刻,小明站在点
,小明和小华的身高都是1.5m, 同一时刻,小明站在点 处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为
处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为 和
和 ,那么塔高
,那么塔高
 .22m
.22m  .13.5m
.13.5m  .24m
.24m 边AB上一点,则下列四个条件不能单独判定
边AB上一点,则下列四个条件不能单独判定 的是( )
的是( ) 



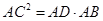
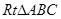 中,
中,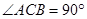 ,
, 是斜边
是斜边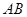 上的中线,
上的中线, ,
,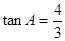 ,点
,点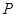 是
是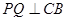 ,交
,交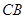 延长线于点
延长线于点 ,
,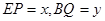 .
.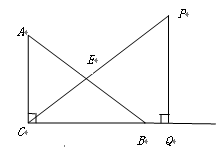
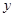 关于
关于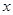 的函数关系式及定义域;(4分)
的函数关系式及定义域;(4分)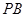 ,当
,当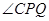 时,求
时,求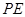 的长;(4分)
的长;(4分) 作
作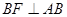 交
交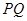 于
于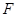 ,当
,当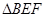 和
和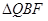 相似时,求
相似时,求 的值.(6分)
的值.(6分)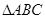 中,
中,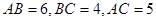 ,点
,点 在边
在边 上,
上,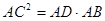 ,那么
,那么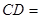 ▲
▲ 
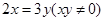 ,则下列比例式成立的是
,则下列比例式成立的是 
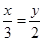
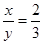



 =BF.
=BF.